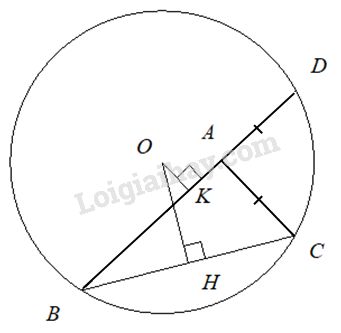
Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 3 - Hình học 9

Đề bài

Cho tam giác ABC. Trên tia đối của tia AC lấy điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp ∆BDC. Từ O lần lượt kẻ các đường vuông góc OH, OK với BC và BD ( H $\in$ BC, K $\in$ BD).

a) Chứng minh OH > OK.

b) So sánh hai cung nhỏ $\overparen{ BD}$ và $\overparen{ BC}.$

Lời giải chi tiết

a) Trong ∆ABC, theo bất đẳng thức tam giác:

$BC < AB + AC = AB + AD = BD$ ( vì $AC = AD$)

$\Rightarrow OH > OK$ ( định lí liên hệ giữa dây cung và khoảng cách đến tâm).

b) Vì $BC < BD$ (cmt) $\Rightarrow \overparen{BC}<\overparen{BD}$

 HocTot.Nam.Name.Vn