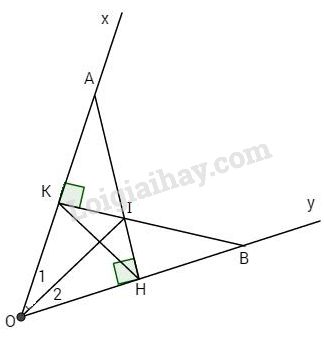
Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 2 - Hình học 7

Đề bài

Cho góc nhọn  \(\widehat {xOy}\), lấy A thuộc Ox, B thuộc Oy sao cho OA = OB, kẻ AH vuông góc với Oy và BK vuông góc với Ox.

a) Chứng minh \(\Delta OHK\) cân.

b) Gọi I là giao điểm của AH và BK. Chứng minh OI là tia phân giác của \(\widehat {xOy}\).

Lời giải chi tiết

a) Xét hai tam giác vuông OHA và OKB có:

+) \(\widehat O\) chung,

+) \(OA = OB\) (giả thiết)

Vậy \(\Delta OHA = \Delta OKB\) (g.c.g)

\( \Rightarrow OH = OK\) (cạnh tương ứng)

Vậy tam giác OHK cân tại O.

b) Ta có OA = OB (giả thiết),

OK = OH (chứng minh trên)

\( \Rightarrow OA - OK = OB - OH\) hay \(AK = HB.\)          (1)

Xét hai tam giác vuông IKA và IHB có AK = HB (chứng minh trên)

Và \(\widehat {KAI} = \widehat {HBI}\) (chứng minh trên)

\( \Rightarrow \Delta IKA = \Delta IHB\) (g.c.g)

Do đó IA = IB (chứng minh trên)

Xét \(\Delta OIA \) và \( \Delta OIB\) có:

+) IO chung

+) OA= OB (giả thiết)

+) IA = IB (chứng minh trên)

\( \Rightarrow \Delta OIA = \Delta OIB\) (c.c.c)

\( \Rightarrow \widehat {AOI} = \widehat {BOI}\) (2 góc tương ứng)

Hay OI là tia phân giác của \(\widehat {xOy}\).

HocTot.Nam.Name.Vn