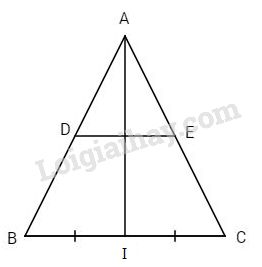
Đề kiểm tra 15 phút - Đề số 2 - Bài 6 - Chương 2 - Hình học 7

Đề bài

Cho tam giác ABC cân tại A, trên các cạnh AB và AC lấy tương ứng hai điểm D và E sao cho AD = AE.

a) Chứng minh rằng DE // BC.

b) Gọi I là trung điểm của BC. Chứng minh AI là đườngt rung trực của đoạn BC.

Lời giải chi tiết

a) Ta có AD = AE (giả thiết), nên tam giác ADE cân tại A và $\widehat A + \widehat {ADE} + \widehat {AED} = {180^o}$

$\widehat {ADE} = \widehat {AED} = {{{{180}^o} - \widehat A} \over 2}$   (1)

Tương tự tam giác ABC cân tại A nên

$\widehat {ABC} = \widehat {ACB} = {{{{180}^o} - \widehat A} \over 2}$

Từ (1) và (2) $\Rightarrow \widehat {ADE} = \widehat {ABC}$.

Do đó DE // BC (cặp góc đồng vị bằng nhau).

b) Xét $\Delta AIB$ và $\Delta AIC$ có:

+) AI cạnh chung,

+) IB = IC (giả thiết),

+) AB  = AC (giả thiết)

$\Rightarrow \Delta AIB = \Delta AIC$ (c.c.c)

$\Rightarrow \widehat {AIB} = \widehat {AIC} = {90^o}$ hay $AI \bot BC.$

Mặt khác I là trung điểm của BC (giả thiết).

Vậy AI là đường trung trực của đoạn thẳng BC.

HocTot.Nam.Name.Vn