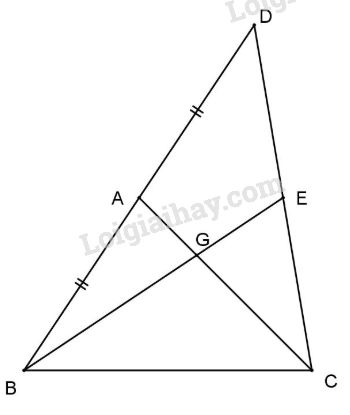
Đề kiểm tra 15 phút - Đề số 1 - Bài 4 - Chương 3 – Hình học 7Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 4 - Chương 3 – Hình học 7 Đề bài Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho \(AD = AB.\) Trên cạnh AC lấy điểm G sao cho \(AG = \dfrac{1}{ 3}AC.\) Gọi E là giao điểm của BG và DC. Chứng minh rằng E là trung điểm của CD Phương pháp giải - Xem chi tiết Sử dụng tính chất đường trung tuyến trong tam giác Lời giải chi tiết
Ta có \(A{\rm{D}} = AB\) (gt) nên CA là đường trung tuyến của \(\Delta BC{\rm{D}}\), lại có \(AG =\dfrac {1 }{ 3}AC\) (gt) nên G là trọng tâm của \(\Delta BC{\rm{D}}.\) Vì BG cắt CD tại E nên BE là trung tuyến của \(\Delta BC{\rm{D}}\). Do đó E là trung điểm của CD. HocTot.Nam.Name.Vn
|