Đề kiểm tra 15 phút – Chương 2 – Đề số 5 – Đại số và giải tích 11

Câu 1:

Theo yêu cầu bài toán:

+ 3 câu đầu phải được chọn thì chỉ có 1 cách

+ Chọn 7 câu trong 17 câu còn lại có: \(C_{17}^7\) cách

Vậy có \(C_{17}^7\) cách.

Chọn đáp án D.

Câu 2:

Điều kiện: \(n \ge 9\)

Ta có: \(C_n^6 + 3C_n^7 + 3C_n^8 + C_n^9 = 2C_{n + 2}^8\)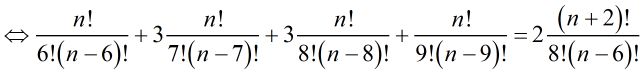

Giải phương trình này có: \(n = 15\)

Chọn đáp án C.

Câu 3:

Ta có: \(\left\{ \begin{array}{l}C_{10}^4 + C_{11}^4 = 540\\C_{11}^5 = 462\end{array} \right.\)\(\, \Rightarrow C_{10}^4 + C_{11}^4 \ne C_{11}^5 = 462\)

Chọn đáp án D.

Câu 4:

Điều kiện: \(x \ge 2\)

Ta có: \(A_x^2 = 110 \Leftrightarrow \dfrac{{x!}}{{\left( {x - 2} \right)!}} = 110\)

\( \Leftrightarrow x\left( {x - 1} \right) = 110 \Rightarrow x = 11\)

Chọn B

Câu 5:

Số véc tơ khác véc tơ không có điểm đầu và điểm cuối thuộc 2010 điểm đã cho là \(C_{2010}^2 = 4038090\) (cách)

Chọn đáp án B.

Câu 6:

Ta có: \(C_n^{n - k} = 28 \Leftrightarrow \dfrac{{n!}}{{\left( {n - k} \right)!k!}} = 28\)\( \Leftrightarrow \left\{ \begin{array}{l}n = 8\\k = 2\end{array} \right.\)

Chọn đáp án C.

Câu 7:

Số đường chéo của đa giác được xác định bởi công thức

\(\dfrac{{n\left( {n - 3} \right)}}{2} = 44 \)

\(\Leftrightarrow {n^2} - 3n - 88 = 0\)

\(\Leftrightarrow \left[ \begin{array}{l}n = 11\\n =  - 8\end{array} \right.\)

Chọn đáp án A.

Câu 8:

Điều kiện: \(n \ge 3\)

Ta có: \(A_n^3 = 20n \Leftrightarrow \dfrac{{n!}}{{\left( {n - 3} \right)!}} = 20n\)

\(\Leftrightarrow n\left( {n - 1} \right)\left( {n - 2} \right) = 20n\)

\( \Leftrightarrow \left( {n - 1} \right)\left( {n - 2} \right) = 20 \Leftrightarrow \left[ \begin{array}{l}n = 6\\n =  - 3\end{array} \right.\)

Chọn đáp án A.

Câu 9:

Số đường chéo của đa giác được xác định bằng công thức:

\(\dfrac{{n\left( {n - 3} \right)}}{2} = 135\)

\(\Leftrightarrow {n^2} - 3n - 270 = 0 \)

\(\Leftrightarrow \left[ \begin{array}{l}n = 18\\n =  - 15\end{array} \right.\)

Chọn đáp án D.

Câu 10:

Điều kiện: \(n \ge 2\)

Ta có: \(\dfrac{{C_{n + 1}^2}}{{C_n^2}} \ge \dfrac{3}{{10}}n\)

\(\Leftrightarrow \dfrac{{\dfrac{{\left( {n + 1} \right)!}}{{2!\left( {n - 1} \right)!}}}}{{\dfrac{{n!}}{{2!\left( {n - 2} \right)!}}}} \ge \dfrac{3}{{10}}n \)

\(\Leftrightarrow \dfrac{{n\left( {n + 1} \right)}}{{n\left( {n - 1} \right)}} \ge \dfrac{3}{{10}}n\)

\( \Leftrightarrow \dfrac{{n + 1}}{{n - 1}} \ge \dfrac{3}{{10}}n \)

\(\Leftrightarrow 10n + 10 \ge 3{n^2} - 3n\)

\( \Leftrightarrow 3{n^2} - 13n - 10 \le 0\)

\(\Leftrightarrow  - \dfrac{2}{3} \le n \le 5\)

Chọn đáp án D

HocTot.Nam.Name.Vn