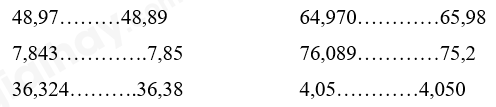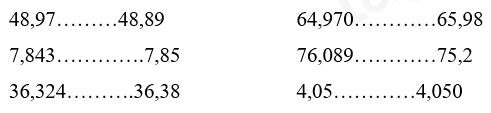Đề cương ôn tập học kì 2 Toán 5Tải vềTính nhẩm: a) 112,4 x 10 = ..... Một thửa ruộng hình thang có trung bình cộng hai đáy là 75m ....
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
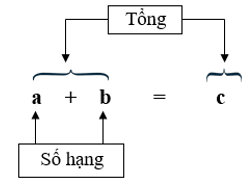
LÝ THUYẾT I. SỐ TỰ NHIÊN, PHÂN SỐ, SỐ THẬP PHÂN 1. Phép cộng:
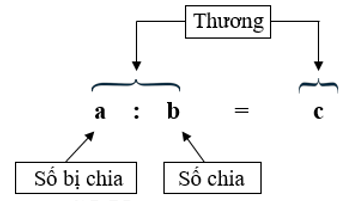
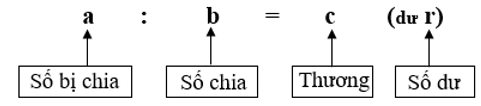
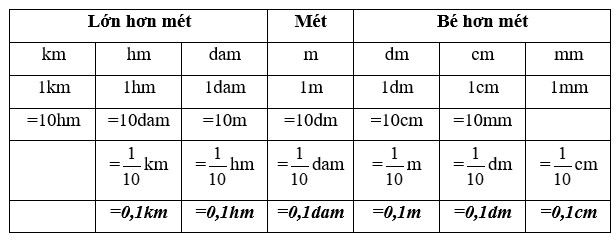
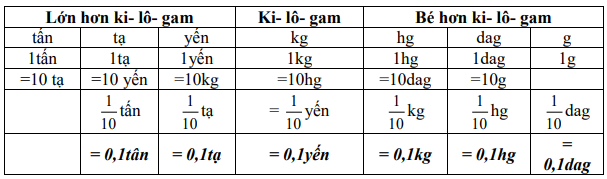
Phép cộng các số tự nhiên, phân số, số thập phân đều có các tính chất sau: Tính chất kết hợp: (a + b) + c = a + (b + c) Cộng với 0: a + 0 = 0 + a = a a – a = 0 a – 0 = a 3. Phép nhân Phép nhân các số tự nhiên, phân số, số thập phân đều có các tính chất sau: Tính chất kết hợp: (a x b) x c = a x (b x c) Nhân một tổng với một số: (a + b) x c = a x c + b x c Phép nhân có thừa số bằng 1: 1 x a = a x 1 = a Phép nhân có thừa số bằng 0: 0 x a = a x 0 = 0 4. Phép chia a) Trong phép chia hết: Chú ý: Không có phép chia cho số 0 a : 1 = a a : a = 1 (a khác 0) 0 : b = 0 (b khác 0) b) Trong phép chia có dư: Chú ý: Số dư phải bé hơn số chia II. SỐ ĐO ĐẠI LƯỢNG 1. Bảng đơn vị đo độ dài:
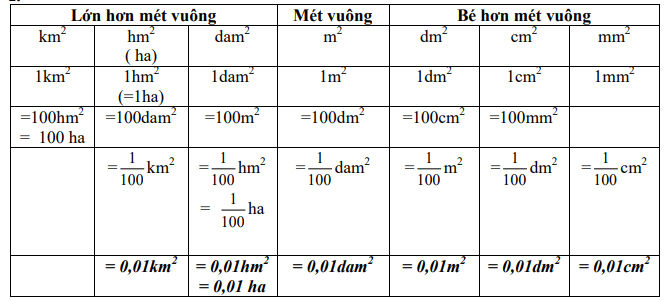
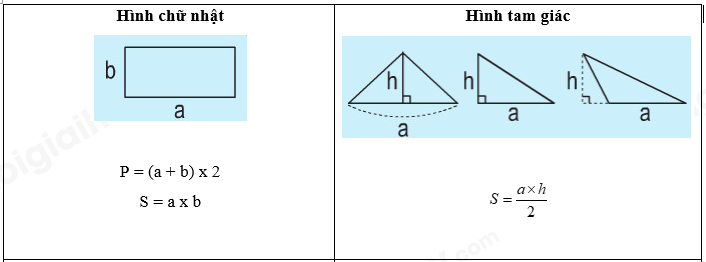
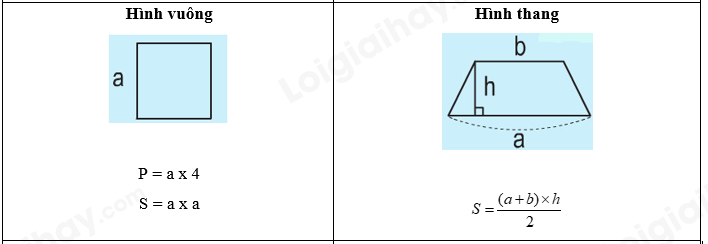
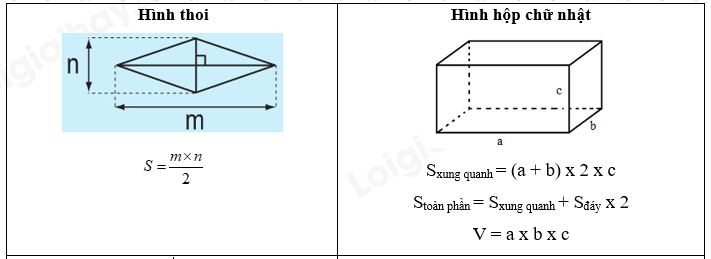
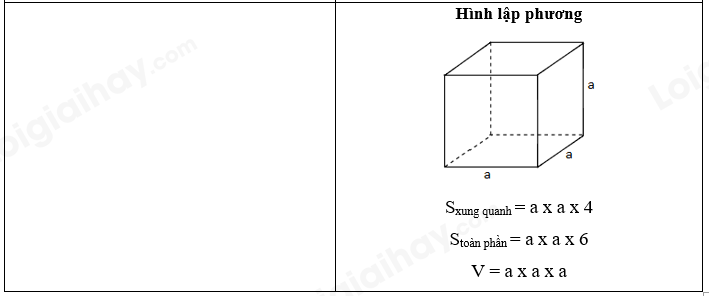
2. Bảng đơn vị đo khối lượng: 3. Bảng đơn vị đo diện tích: 4. Bảng đơn vị đo thể tích: III. HÌNH HỌC IV. ÔN TẬP VỀ GIẢI TOÁN 1. Tỉ số phần trăm - Tính tỉ số phần trăm của hai số A và B: A : B x 100 - Tính tỉ số phần trăm của một số A: Giá trị phần trăm = Số A : 100 x số phần trăm Giá trị phần trăm = Số A x số phần trăm : 100 - Tìm một số A khi biết giá trị phần trăm của số đó: Số A = Giá trị phần trăm: số phần trăm x 100 Số A = Giá trị phần trăm x 100 : số phần trăm 2. Bài toán chuyển động đều - Vận tốc: v = s : t - Quãng đường: s = v x t - Thời gian: t = s : v - Bài toán hai xe chuyển động ngược chiều, xuất phát cùng lúc - Thời gian để hai xe gặp nhau: t = s : (v1 + v2) - Thời điểm hai xe gặp nhau = Thời điểm khởi hành + thời gian đi đến chỗ gặp nhau - Vị trí 2 xe gặp nhau cách A là: s1 = v1 x t - Bài toán hai xe chuyển động cùng chiều, xuất phát cùng thời điểm - Thời gian để hai đuổi kịp nhau: t = s : (v1 - v2) - Thời điểm hai xe gặp nhau = Thời điểm khởi hành + thời gian đi đến chỗ gặp nhau - Vị trí gặp nhau cách A là s1 = v1 x t BÀI TẬP 1. Số tự nhiên, phân số, hỗn số, số thập phân Câu 1. Tính a) $2 + \frac{3}{4}$ b) $\frac{1}{3} + \frac{3}{2} - \frac{7}{4}$ c) $\frac{1}{6} + \frac{3}{8} - \frac{1}{4}$ d) $\frac{5}{{12}} + \frac{3}{8} \times \frac{4}{9}$ e) $\frac{4}{5} - \frac{1}{5} \times \frac{7}{2}$ f) $\frac{{16}}{9} - \frac{4}{{15}}:\frac{2}{5}$ Câu 2. Điền dấu >, <, = Câu 3. Đặt tính rồi tính a) 247,06 + 316,492 b) 152,47 + 93 c) 642,78 – 21,472 d) 91,4 – 82 e) 0,524 x 304 f) 112,56 : 28 Câu 4. Tính nhẩm: a) 112,4 x 10 = ..... ; b) 112,5 x 0,1 = ..... ; c) 68,3 x 100 = ..... d) 68,3 x 0,01 = ..... e) 4,351 x 1000 = ..... f) 4,351 x 0,001 = ..... Câu 5: Viết số thích hợp vào chỗ chấm: Câu 6: Viết số thích hợp vào chỗ chấm: Câu 7. Điền số thích hợp vào chỗ chấm $\frac{1}{5}$ giờ = ……. phút $\frac{1}{3}$ ngày = ……. phút 1,3 giờ = ……. phút $\frac{5}{6}$ phút = ……. giây 4 phút 36 giây = ……. phút 2 giờ 15 phút = ……. giờ Câu 8. Tính chu vi và diện tích hình tròn có: a) Bán kính r = 6 cm b) Đường kính d = 16,8 cm Câu 9. Một thửa ruộng hình thang có trung bình cộng hai đáy là 75m, đáy bé kém đáy lớn 24m, chiều cao bằng $\frac{1}{2}$ đáy lớn. Tính diện tích của thửa ruộng đó. Câu 10. Cho hình vẽ, tính diện tích hình thang IJGH biết diện tích hình tam giác IHF là 6 cm2. Câu 11. Hình thang ABCD có đáy CD = 16cm, đáy bé AB = 9cm. Biết DM = 7cm, diện tích tam giác BMC bằng 37,8cm2. Tính diện tích hình thang ABCD. Câu 12. Đường kính của một bánh xe đạp là 60 cm. Để người đi xe đạp đi được quãng đường 1884m thì mỗi bánh xe phải lăn bao nhiêu vòng? Câu 13. Cho hình vuông ABCD có chu vi 48dm. Tính diện tích phần tô đậm trong hình dưới đây. Câu 14. Một bể nuôi cá hình hộp chữ nhật có chiều dài 2,5m, chiều rộng 1,6m và chiều cao 1,4m. a) Tính diện tích kính dùng làm bể cá đó (bể không nắp). b) Mực nước trong bể cao bằng $\frac{3}{4}$ chiều cao của bể. Hỏi trong bể chứa bao nhiêu lít nước? (biết 1 lít = 1dm3) Câu 15. Một bể nước hình hộp chữ nhật có chiều dài 4,5m; chiều rộng là 2,5m và chiều cao 1,8m a) Tính diện tích xung quanh và diện tích toàn phần của bể nước đó. b) Bể đó chứa được nhiều nhất bao nhiêu lít nước? c) Trong bể đang có 16,2m3 nước. Tính chiều cao của mực nước trong bể. Câu 16: Một phòng học dạng hình hộp chữ nhật có chiều dài 8m, chiều rộng 6m, chiều cao 3,5m. Người ta muốn sơn trần nhà và bốn bức tường phía trong phòng học. a) Tính diện tích cần sơn biết diện tích các cửa là 15m. b) Mỗi mét vuông sơn với giá 25 000 đồng. Hỏi sơn phòng học đó hết tất cả bao nhiêu tiền? Câu 17. Một hình lập phương có diện tích toàn phần là 384cm2. Tính thể tích hình lập phương. Câu 18. Một bể nước hình lập phương (không có nắp) có cạnh 0,6m. a) Tính diện tích toàn phần của bể nước. b) Trong bể đang chứa nước đến $\frac{2}{3}$ bể. Hỏi phải đổ thêm mấy lít nước thì đầy bể. Biết 1 lít = 1 dm3 Câu 19. Một người bỏ ra 2 000 000 đồng để mua hoa quả về bán. Sau khi bán hết, người đó thu về 2 800 000 đồng. Hỏi người bán hoa quả đã lãi bao nhiêu phần trăm so với tiền vốn bỏ ra? Câu 20. Tháng vừa qua, xí nghiệp may được 7500 bộ quần áo. Tính ra xí nghiệp đã đạt 120% kế hoạch ban đầu. Hỏi tháng vừa qua, xí nghiệp đã may nhiều hơn so với kế hoạch ban đầu bao nhiêu bộ quần áo? Câu 21: Trại nuôi ong vừa mới thu hoạch mật ong. Sau khi người ta bán đi 135l mật ong thì lượng mật ong còn lại bằng 62,5% lượng mật ong vừa thu hoạch. a) Hỏi trại đó còn lại bao nhiêu lít mật ong? b) Người ta đem lượng mật ong còn lại đổ hết vào các chai, mỗi chai chứa 0,75 lít mật. Hỏi có tất cả bao nhiêu chai mật ong? Câu 22. Lãi suất tiết kiệm của ngân hàng là 0,6% một tháng. Biết rằng mỗi tháng chị Mai đều đi rút tiền lãi và nhận về được 120 000 đồng. Hỏi chị Mai đã gửi bao nhiêu tiền vào quỹ tiết kiệm? Câu 23: Một ô tô đi từ tỉnh A lúc 6 giờ và đến B lúc 10 giờ 45 phút. Ô tô đi với vận tốc 48 km/giờ và nghỉ dọc đường mất 15 phút. Tính độ dài quãng đường từ tỉnh A đến tỉnh B. Câu 24: Ô tô và xe máy khởi hành cùng một lúc và đi ngược chiều nhau. Ô tô đi từ A với vận tốc 44,5km/ giờ, xe máy đi từ B với vận tốc 32,5 km/giờ. Sau 1 giờ 30 phút ô tô và xe máy gặp nhau tại C. Hỏi quãng đường AB dài bao nhiêu ki-lô-mét? Câu 25: Một xe máy đi từ A đến B với vận tốc 40km/giờ. Sau khi xe máy đi được 30 phút thì một ô tô cũng đi từ A đến B với vận tốc 60km/giờ. a) Sau bao lâu thì ô tô đuổi kịp xe máy? b) Điểm gặp nhau cách A bao nhiêu ki-lô-mét? Câu 26. Lúc 7 giờ một xe máy đi từ A đến B với vận tốc 45km/giờ. Một lúc sau một xe taxi cũng xuất phát từ A để đi tới B. Hai xe gặp nhau ở địa điểm cách B là 22,5km. Biết rằng quãng đường từ A tới B dài 180km. Hỏi: a) Xe máy cứ đi như thế thì tới B lúc mấy giờ? b) Hai xe gặp nhau lúc mấy giờ? HƯỚNG DẪN GIẢI Câu 1. Tính a) $2 + \frac{3}{4}$ b) $\frac{1}{3} + \frac{3}{2} - \frac{7}{4}$ c) $\frac{1}{6} + \frac{3}{8} - \frac{1}{4}$ d) $\frac{5}{{12}} + \frac{3}{8} \times \frac{4}{9}$ e) $\frac{4}{5} - \frac{1}{5} \times \frac{7}{2}$ f) $\frac{{16}}{9} - \frac{4}{{15}}:\frac{2}{5}$ Phương pháp giải Đối với biểu thức có chứa phép tính cộng, trừ, nhân, chia ta thực hiện phép tính nhân, chia trước, thực hiện phép tính cộng, trừ sau. Lời giải chi tiết a) $2 + \frac{3}{4} = \frac{8}{4} + \frac{3}{4} = \frac{{11}}{4}$ b) $\frac{1}{3} + \frac{3}{2} - \frac{7}{4} = \frac{4}{{12}} + \frac{{18}}{{12}} - \frac{{21}}{{12}} = \frac{1}{{12}}$ c) $\frac{1}{6} + \frac{3}{8} - \frac{1}{4} = \frac{4}{{24}} + \frac{9}{{24}} - \frac{6}{{24}} = \frac{7}{{24}}$ d) $\frac{5}{{12}} + \frac{3}{8} \times \frac{4}{9} = \frac{5}{{12}} + \frac{{3 \times 4}}{{8 \times 9}} = \frac{5}{{12}} + \frac{{3 \times 4}}{{4 \times 2 \times 3 \times 3}} = \frac{5}{{12}} + \frac{1}{6} = \frac{7}{{12}}$ e) $\frac{4}{5} - \frac{1}{5} \times \frac{7}{2} = \frac{4}{5} - \frac{7}{{10}} = \frac{8}{{10}} - \frac{7}{{10}} = \frac{1}{{10}}$ f) $\frac{{16}}{9} - \frac{4}{{15}}:\frac{2}{5} = \frac{{16}}{9} - \frac{4}{{15}} \times \frac{5}{2} = \frac{{16}}{9} - \frac{{20}}{{30}} = \frac{{16}}{9} - \frac{2}{3} = \frac{{16}}{9} - \frac{6}{9} = \frac{{10}}{9}$ Câu 2. Điền dấu >, <, = Phương pháp - Số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn. - Nếu phần nguyên của hai số đó bằng nhau, thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn. Cách giải
Câu 3. Đặt tính rồi tính a) 247,06 + 316,492 b) 152,47 + 93 c) 642,78 – 21,472 d) 91,4 – 82 e) 0,524 x 304 f) 112,56 : 28 Phương pháp Đặt tính rồi tính theo các quy tắc đã học. Cách giải
Câu 4. Tính nhẩm: a) 112,4 x 10 = ..... ; b) 112,5 x 0,1 = ..... ; c) 68,3 x 100 = ..... d) 68,3 x 0,01 = ..... e) 4,351 x 1000 = ..... f) 4,351 x 0,001 = ..... Phương pháp - Muốn nhân một số thập phân với 10, 100, 1000, … ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, …. chữ số. - Muốn nhân một số thập phân với 0,1, 0,01, 0,001, … ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, …. chữ số. Cách giải a) 112,4 x 10 = 1124; b) 112,5 x 0,1 = 11,25; c) 68,3 x 100 = 6830 d) 68,3 x 0,01 = 0,683 e) 4,351 x 1000 = 4351 f) 4,351 x 0,001 = 0,004351 2. Số đo đại lượng Câu 5: Viết số thích hợp vào chỗ chấm: a) 3kg 275g = ………kg b) 3268g = ……… kg c) 5tấn 114kg = ……… kg d) 2tấn 5tạ = …….. tấn e) 4kg 65g = ……. kg f) 789 g = …….. kg g) 3 tạ = ……. tấn Phương pháp Áp dụng cách đổi: 1g = 0,001 kg ; 1 kg = 0,001 tấn 1 tạ = 0,1 tấn Cách giải a) 3kg 275g = 3,275kg b) 3268g = 3,268 kg c) 5tấn 114kg = 5,114 kg d) 2tấn 5tạ = 2,5 tấn e) 4kg 65g = 4,065 kg f) 789 g = 0,789 kg g) 3 tạ = 0,3 tấn Câu 6: Viết số thích hợp vào chỗ chấm: 8,56 dm2 = …… cm2 1,8 ha = ………. m2 7ha 68m2 = ………ha 1m2 25cm2 = ………. cm2 8 dam2 = ……. m2 4350m2 = ………. ha 37m2 4cm2 = …….. dm2 3 ha = ……. km2 Phương pháp Áp dụng cách đổi 1dm2 = 100cm2 ; 1 ha = 10000m2 1dam2 = 100m2 ; 1 ha = 0,01km2 Cách giải 8,56 dm2 = 856 cm2 1,8 ha = 18000 m2 7ha 68m2 = 7,0068 ha 1m2 25cm2 = 10 025 cm2 8 dam2 = 800 m2 4350m2 = 0,435 ha 37m2 4cm2 = 3700,04 dm2 3 ha = 0,03 km2
Câu 7. Điền số thích hợp vào chỗ chấm $\frac{1}{5}$ giờ = ……. phút $\frac{1}{3}$ ngày = ……. phút 1,3 giờ = …….. phút $\frac{5}{6}$ phút = ……. giây 4 phút 36 giây = ……. phút 2 giờ 15 phút = ……. giờ Phương pháp Áp dụng cách đổi: 1 giờ = 60 phút ; 1 phút = 60 giây Cách giải $\frac{1}{5}$ giờ = $\frac{1}{5} \times 60$ phút = 12 phút $\frac{1}{3}$ ngày = 8 giờ = 8 x 60 phút = 480 phút 1,3 giờ = 1,3 x 60 phút = 78 phút $\frac{5}{6}$ phút = $\frac{5}{6} \times 60$giây = 50 giây 4 phút 36 giây = $4\frac{{36}}{{60}}$ phút = $4\frac{3}{5}$ phút = 4,6 phút 2 giờ 15 phút = $2\frac{{15}}{{60}}$ giờ = $2\frac{1}{4}$ giờ = 2,25 giờ 3. Hình học Câu 8. Tính chu vi và diện tích hình tròn có: a) Bán kính r = 6 cm b) Đường kính d = 16,8 cm Phương pháp Chu vi hình tròn = d x 3,14 = r x 2 x 3,14 Diện tích hình tròn = r x r x 3,14 Cách giải a) Chu vi hình tròn có bán kính 6 cm là 6 x 2 x 3,14 = 37,68 (cm) Diện tích hình tròn có bán kính 6 cm là 6 x 6 x 3,14 = 113,04 (cm2) Đáp số: Chu vi: 37,68 cm; Diện tích: 113,04 cm2 b) Chu vi hình tròn có đường kính 16,8 cm là 16,8 x 2 = 33,6 (cm) Bán kính hình tròn là 16,8 : 2 = 8,4 (cm) Diện tích hình tròn là 8,4 x 8,4 x 3,14 = 221,5584 (cm2) Đáp số: Chu vi: 33,6 cm Diện tích: 221,5584 cm2
Câu 9. Một thửa ruộng hình thang có trung bình cộng hai đáy là 75m, đáy bé kém đáy lớn 24m, chiều cao bằng $\frac{1}{2}$ đáy lớn. Tính diện tích của thửa ruộng đó. Phương pháp giải - Tìm tổng độ dài hai đáy = Trung bình cộng hai đáy x 2 - Đáy lớn = (tổng + hiệu) : 2 - Chiều cao = đáy lớn : 2 - Diện tích thửa ruộng hình thang = tổng độ dài hai đáy x chiều cao : 2 Cách giải Tổng độ dài hai đáy là 75 x 2 = 150 (m) Độ dài đáy lớn là (150 + 24) : 2 = 87 (m) Chiều cao của hình thang là 87: 2 = 43,5 (m) Diện tích thửa ruộng đó là 150 x 43,5 : 2 = 3262,5 (m2) Đáp số: 3262,5 m2
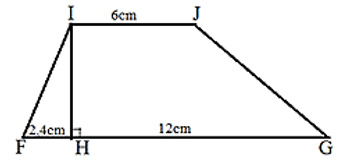
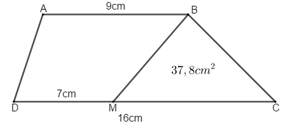
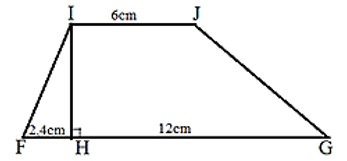
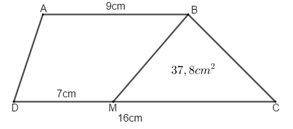
Câu 10. Cho hình vẽ, tính diện tích hình thang IJGH biết diện tích hình tam giác IHF là 6 cm2. Phương pháp - Chiều cao IH = 2 x diện tích tam giác IHF : độ dài cạnh HF - Diện tích hình thang = $\frac{{(IJ + HG) \times IH}}{2}$ Cách giải Độ dài đường cao IH là: 6 x 2 : 2,4 = 5 (cm) Diện tích hình thang IJGH là: (6 + 12) x 5 : 2 = 45 (cm2) Đáp số: 45cm2 Câu 11. Hình thang ABCD có đáy CD = 16cm, đáy bé AB = 9cm. Biết DM = 7cm, diện tích tam giác BMC bằng 37,8cm2. Tính diện tích hình thang ABCD. Phương pháp - Tìm độ dài MC = DC – DM - Tìm độ dài đường cao của tam giác BMC = Diện tích tam giác BMC x 2 : độ dài MC - Diện tích hình thang ABCD = (AB + CD) x chiều cao : 2 Cách giải Độ dài đáy MC của tam giác BMC là 16 – 7 = 9 (cm) Độ dài đường cao của tam giác MBC là 37,8 x 2 : 9 = 8,4 (cm) Diện tích hình thang ABCD là (16 + 9) x 8,4 : 2 = 105 (cm2) Đáp số: 105 cm2 Câu 12. Đường kính của một bánh xe đạp là 60 cm. Để người đi xe đạp đi được quãng đường 1884m thì mỗi bánh xe phải lăn bao nhiêu vòng? Phương pháp - Tìm chu vi của bánh xe = Đường kính x 3,14 - Đổi sang đơn vị m - Tìm số vòng = quãng đường : chu vi bánh xe
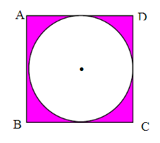
Cách giải Chu vi của bánh xe là 60 x 3,14 = 188,4 (cm) = 1,884 m Để đi được quãng đường 1884m thì mỗi bánh xe phải lăn số vòng là 1884 : 1,884 = 1000 (vòng) Đáp số: 1000 vòng Câu 13. Cho hình vuông ABCD có chu vi 48dm. Tính diện tích phần tô đậm trong hình dưới đây. Phương pháp - Tìm độ dài cạnh hình vuông = Chu vi : 4 - Tìm diện tích hình vuông = cạnh x cạnh - Tìm bán kính hình tròn = Độ dài cạnh hình vuông : 2 - Diện tích hình tròn = r x r x 3,14 - Tìm diện tích phần tô đậm = Diện tích hình vuông – diện tích hình tròn Cách giải Cạnh của hình vuông là 48 : 4 = 12 (dm) Diện tích hình vuông là 12 x 12 = 144 (dm2) Bánh kính hình tròn là 12 : 2 = 6 (dm) Diện tích hình tròn là 6 x 6 x 3,14 = 113,04 (dm2) Diện tích phần tô đậm là 144 - 113,04 = 30,96 (dm2) Đáp số: 30,96 dm2
Câu 14. Một bể nuôi cá hình hộp chữ nhật có chiều dài 2,5m, chiều rộng 1,6m và chiều cao 1,4m. a) Tính diện tích kính dùng làm bể cá đó (bể không nắp). b) Mực nước trong bể cao bằng $\frac{3}{4}$ chiều cao của bể. Hỏi trong bể chứa bao nhiêu lít nước? (biết 1 lít = 1dm3) Phương pháp a) Diện tích xung quanh = (chiều dài + chiều rộng) x 2 x chiều cao Diện tích 1 mặt đáy = chiều dài x chiều rộng Diện tích kính dùng làm bể cá = Diện tích xung quanh + Diện tích 1 mặt đáy b) Tìm thể tích bể = Chiều dài x chiều rộng x chiều cao Thể tích nước trong bể = thể tích bể x $\frac{3}{4}$ Cách giải a) Diện tích xung quanh của bể cá là (2,5 + 1,6) x 2 x 1,4 = 11,48 (m2) Diện tích 1 mặt đáy là 2,5 x 1,6 = 4 (m2) Diện tích kính dùng làm bể cá đó là 11,48 + 4 = 15,48 (m2) b) Thể tích của bể cá là 2,5 x 1,6 x 1,4 = 5,6 (m3) = 5600dm3 = 5600 lít Trong bể chứa số lít nước là $5600 \times \frac{3}{4} = 4200$ (lít) Đáp số: a) 15,48 m2 ; b) 4200 lít Câu 15. Một bể nước hình hộp chữ nhật có chiều dài 4,5m; chiều rộng là 2,5m và chiều cao 1,8m a) Tính diện tích xung quanh và diện tích toàn phần của bể nước đó. b) Bể đó chứa được nhiều nhất bao nhiêu lít nước? c) Trong bể đang có 16,2m3 nước. Tính chiều cao của mực nước trong bể. Phương pháp a) Diện tích xung quanh = (chiều dài + chiều rộng) x 2 x chiều cao Diện tích mặt đáy = Chiều dài x chiều rộng Diện tích toàn phần bể nước = Diện tích xung quanh + Diện tích 1 mặt đáy b) Thể tích bể = Chiều dài x chiều rộng x chiều cao c) Chiều cao mực nước = Thể tích nước : diện tích đáy Cách giải a) Diện tích xung quanh của bể nước là (4,5 + 2,5) x 2 x 1,8 = 25,2 (m2) Diện tích mặt đáy của bể là 4,5 x 2,5 = 11,25 (m2) Diện tích toàn phần của bể là 25,2 + 11,25 x 2 = 47,7 (m2) b) Bể đó chứa được nhiều nhất số lít nước là 4,5 x 2,5 x 1,8 = 20,25 (m3) Đổi: 20,25 m3 = 20250 dm3 = 20250 lít c) Chiều cao của mực nước trong bể là 16,2 : 11,25 = 1,44 (m) Đáp số: a) Sxq = 25,2m2 ; Stp = 47,7 m2 b) 20250 lít c) 1,44 m Câu 16: Một phòng học dạng hình hộp chữ nhật có chiều dài 8m, chiều rộng 6m, chiều cao 3,5m. Người ta muốn sơn trần nhà và bốn bức tường phía trong phòng học. a) Tính diện tích cần sơn biết diện tích các cửa là 15m. b) Mỗi mét vuông sơn với giá 25 000 đồng. Hỏi sơn phòng học đó hết tất cả bao nhiêu tiền? Phương pháp a) Diện tích xung quanh = (chiều dài + chiều rộng) x 2 x chiều cao Diện tích trần nhà = Chiều dài x chiều rộng Diện tích cần sơn = Diện tích xung quanh + Diện tích trần nhà – Diện tích các cửa b) Số tiền = 25 000 x Diện tích cần sơn Cách giải a) Diện tích xung quanh của căn phòng là (8 + 6) x 2 x 3,5 = 98 (m2) Diện tích trần nhà là 8 x 6 = 48 (m2) Diện tích cần sơn là 98 + 48 – 15 = 131 (m2) b) Sơn phòng học đó hết tất cả số tiền là 25000 x 131 = 3275000 (m2) Đáp số: a) 131 m2 ; b) 3275000 m2 Câu 17. Một hình lập phương có diện tích toàn phần là 384cm2. Tính thể tích hình lập phương. Phương pháp - Diện tích một mặt của hình lập phương = Diện tích toàn phần : 6 - Tìm độ dài cạnh hình lập phương - Thể tích hình lập phương = cạnh x cạnh x cạnh Cách giải Diện tích một mặt của hình lập phương là 384 : 6 = 64 (cm2) Ta có 64 = 8 x 8 nên độ dài cạnh hình lập phương là 8 cm Thể tích hình lập phương là 8 x 8 x 8 = 512 (cm3) Đáp số: 512 cm3
Câu 18. Một bể nước hình lập phương (không có nắp) có cạnh 0,6m. a) Tính diện tích toàn phần của bể nước. b) Trong bể đang chứa nước đến $\frac{2}{3}$ bể. Hỏi phải đổ thêm mấy lít nước thì đầy bể. Biết 1 lít = 1 dm3 Phương pháp a) Diện tích toàn phần = cạnh x cạnh x 6 b) Thể tích của bể = cạnh x cạnh x cạnh Tìm thể tích nước trong bể = thể tích bể x $\frac{2}{3}$ Tìm thể tích nước cần đổ thêm để đầy bể Cách giải a) Diện tích toàn phần của bể nước là 0,6 x 0,6 x 5 = 1,8 (m2) b) Thể tích bể là: 0,6 x 0,6 x 0,6 = 0,216 (m3) = 216 dm3 = 216 lít Thể tích nước trong bể là $216 \times \frac{2}{3} = 144$(lít) Số lít nước cần đổ thêm để đầy bể là 216 – 144 = 72 (lít) Đáp số: a) 1,8 m2 ; b) 72 lít 4. Ôn tập về giải toán Câu 19. Một người bỏ ra 2 000 000 đồng để mua hoa quả về bán. Sau khi bán hết, người đó thu về 2 800 000 đồng. Hỏi người bán hoa quả đã lãi bao nhiêu phần trăm so với tiền vốn bỏ ra? Phương pháp - Tìm số tiền lãi = Số tiền thu về - Số tiền vốn - Số phần trăm tiền lãi so với tiền vốn = số tiền lãi : số tiền vốn x 100 Cách giải Số tiền lãi là: 2 800 000 – 2 000 000 = 800 000 (đồng) Người đó lãi số phần trăm là: 800 000 : 2000 000 = 0,4 = 40% Đáp số: 40% Câu 20. Tháng vừa qua, xí nghiệp may được 7500 bộ quần áo. Tính ra xí nghiệp đã đạt 120% kế hoạch ban đầu. Hỏi tháng vừa qua, xí nghiệp đã may nhiều hơn so với kế hoạch ban đầu bao nhiêu bộ quần áo? Phương pháp - Tìm số bộ quần áo cần may theo kế hoạch = số bộ quần áo may được thực tế : 120 x 100 - Tìm số bộ quần áo đã may nhiều hơn so với kế hoạch = số bộ quần áo may được thực tế - số bộ quần áo cần may theo kế hoạch Cách giải Số bộ quần áo cần may theo kế hoạch là 7500 : 120 x 100 = 6250 (bộ) Số bộ quần áo đã may nhiều hơn so với kế hoạch là 7500 – 6250 = 1250 (bộ) Đáp số: 1250 bộ quần áo Câu 21: Trại nuôi ong vừa mới thu hoạch mật ong. Sau khi người ta bán đi 135l mật ong thì lượng mật ong còn lại bằng 62,5% lượng mật ong vừa thu hoạch. a) Hỏi trại đó còn lại bao nhiêu lít mật ong? b) Người ta đem lượng mật ong còn lại đổ hết vào các chai, mỗi chai chứa 0,75 lít mật. Hỏi có tất cả bao nhiêu chai mật ong? Phương pháp a) - Tìm số phần trăm lượng mật ong đã bán = 100% - 62,5% - Tìm số lít mật ong ban đầu thu hoạch được = Số lít mật ông đã bán : số phần trăm lượng mật ong đã bán x 100 - Tìm số lít mật ong còn lại b) Số chai = số lít mật ong còn lại : số lít mật ong ở mỗi chai Cách giải a) Coi lượng mật ong thu hoạch được là 100% thì số mật bán đi chiếm số phần trăm là: 100% - 62,5% = 37,5% Lượng mật ong thu hoạch ban đầu là: 135 : 37,5 x 100 = 360 (lít) Lượng mật ong còn lại sau khi bán là: 360 - 135 = 225 (lít) b) Số chai mật ong là: 225 : 0,75 = 300 (chai) Đáp số: a) 225 lít b) 300 chai. Câu 22. Lãi suất tiết kiệm của ngân hàng là 0,6% một tháng. Biết rằng mỗi tháng chị Mai đều đi rút tiền lãi và nhận về được 120 000 đồng. Hỏi chị Mai đã gửi bao nhiêu tiền vào quỹ tiết kiệm? Phương pháp Số tiền gửi = Số liền lãi : phần trăm lãi suất x 100 Cách giải Chị Mai đã gửi bao số tiền vào quỹ tiết kiệm là 120 000 : 0,6 x 100 = 20 000 000 (đồng) Đáp số: 20 000 000 đồng Câu 23: Một ô tô đi từ tỉnh A lúc 6 giờ và đến B lúc 10 giờ 45 phút. Ô tô đi với vận tốc 48 km/giờ và nghỉ dọc đường mất 15 phút. Tính độ dài quãng đường từ tỉnh A đến tỉnh B. Phương pháp - Thời gian ô tô đi = Thời gian đến B – thời gian xuất phát – thời gian nghỉ - quãng đường = vận tốc x thời gian Cách giải Thời gian ô tô đi từ A đến B là 10 giờ 45 phút – 6 giờ - 15 phút = 4 giờ 30 phút = 4,5 giờ Độ dài quãng đường từ tỉnh A đến tỉnh B là 48 x 4,5 = 216 (km) Đáp số: 216 km Câu 24: Ô tô và xe máy khởi hành cùng một lúc và đi ngược chiều nhau. Ô tô đi từ A với vận tốc 44,5km/ giờ, xe máy đi từ B với vận tốc 32,5 km/giờ. Sau 1 giờ 30 phút ô tô và xe máy gặp nhau tại C. Hỏi quãng đường AB dài bao nhiêu ki-lô-mét? Phương pháp - Tìm tổng vận tốc hai xe - Quãng đường = tổng vận tốc x thời gian Cách giải Tổng vận tốc của hai xe là 44,5 + 32,5 = 77 (km) Đổi 1 giờ 30 phút =1,5 giờ Quãng đường AB dài số ki-lô-mét là 77 x 1,5 = 115,5 (km) Đáp số: 115,5 km Câu 25: Một xe máy đi từ A đến B với vận tốc 40km/giờ. Sau khi xe máy đi được 30 phút thì một ô tô cũng đi từ A đến B với vận tốc 60km/giờ. a) Sau bao lâu thì ô tô đuổi kịp xe máy? b) Điểm gặp nhau cách A bao nhiêu ki-lô-mét? Phương pháp a) Tìm quãng đường xe máy đi trước ô tô = vận tốc xe máy x 0,5 giờ Tìm hiệu vận tốc hai xe Thời gian để ô tô đuổi kịp xe máy = Quãng đường xe máy đi trước ô tô : Hiệu vận tốc b) Điểm gặp nhau cách A = vận tốc xe máy x thời gian đi đến chỗ gặp nhau Cách giải a) Đổi 30 phút = 0,5 giờ Trong 30 phút xe máy đi được quãng đường là 40 x 0,5 = 20 (km) Hiệu vận tốc hai xe là 60 – 40 = 20 (km) Thời gian để ô tô đuổi kịp xe máy là 20 : 20 = 1 (giờ) b) Điểm gặp nhau cách A số km là 60 x 1 = 60 (km) Đáp số: a) 1 giờ ; b) 60km Câu 26. Lúc 7 giờ một xe máy đi từ A đến B với vận tốc 45km/giờ. Một lúc sau một xe taxi cũng xuất phát từ A để đi tới B. Hai xe gặp nhau ở địa điểm cách B là 22,5km. Biết rằng quãng đường từ A tới B dài 180km. Hỏi: a) Xe máy cứ đi như thế thì tới B lúc mấy giờ? b) Hai xe gặp nhau lúc mấy giờ? Phương pháp a) Thời gian xe máy đi từ A đến B = quãng đường : vận tốc b) Tìm quãng đường xe máy đi từ A đến địa điểm gặp nhau Tìm thời gian xe máy đi đến chỗ gặp nhau Tìm thời điểm hai xe gặp nhau Cách giải a) Thời gian xe máy đi hết quãng đường AB là 180 : 45 = 4 (giờ) Xe máy đi tới B lúc: 7 giờ + 4 giờ = 11 giờ b) Thời gian xe máy đi đến lúc gặp xe taxi là: (180 - 22,5) : 45 = 3,5 (giờ) = 3 giờ 30 phút Hai xe gặp nhau lúc: 7 giờ + 3 giờ 30 phút = 10 giờ 30 phút Đáp số: a) 11 giờ; b) 10 giờ 30 phút.
|