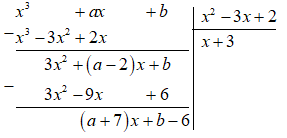Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho hai đa thức \(P\left( x \right) = {x^3} + ax + b\) và \(Q\left( x \right) = {x^2} - 3x + 2\). Xác định các hệ số a, b sao cho với mọi giá trị của x thì \(P\left( x \right) \vdots Q\left( x \right)\).
- A \(a = 7\,;\,\,\,b = - 6\)
- B \(a = - 4\,;\,\,\,b = 5\)
- C \(a = 4\,;\,\,\,b = - 5\)
- D \(a = - 7\,;\,\,\,b = 6\)
Phương pháp giải:
Thực hiện phép chia đa thức \(P\left( x \right)\) cho \(Q\left( x \right)\). Để \(P\left( x \right) \vdots Q\left( x \right)\) thì phép chia đó phải có số dư bằng 0.
Lời giải chi tiết:
Cho hai đa thức \(P\left( x \right) = {x^3} + ax + b\) và \(Q\left( x \right) = {x^2} - 3x + 2\). Xác định các hệ số a, b sao cho với mọi giá trị của x thì \(P\left( x \right) \vdots Q\left( x \right)\).
Để \(P\left( x \right) \vdots Q\left( x \right)\) với mọi giá trị của x\( \Leftrightarrow \left( {a + 7} \right)x + b - 6 = 0\) với mọi giá trị của x
\( \Leftrightarrow \left\{ \begin{array}{l}a + 7 = 0\\b - 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 7\\b = 6\end{array} \right.\)
Vậy với \(a = - 7\) và \(b = 6\) thì \(P\left( x \right) \vdots Q\left( x \right)\) với mọi giá trị của x.
Chọn D.