Nội dung Tổng hợp
Câu hỏi:
Cho hàm số y=(m+2)x+2m2+1 (m là tham số)
a) Vẽ đồ thị hàm số trên khi m=−1.
b) Tìm m để hai đường thẳng (d)y=(m+2)x+2m2+1 và (d′):y=3x+3 cắt nhau tại một điểm trên trục tung.
- A 1
- B −1
- C ±1
- D 0
Phương pháp giải:
a) Thay m=−1 vào hàm số, ta được một hàm số bậc nhất, đồ thị của hàm số bậc nhất là một đường thẳng, ta xác định hai điểm thuộc đồ thị hàm số, kẻ đường thẳng đi qua hai điểm đó thì ta được đồ thị hàm số cần vẽ.
b) Xác định giao điểm của đồ thị hàm số (d′):y=3x+3 với trục tung.
Vì theo đề bài(d)y=(m+2)x+2m2+1và (d′):y=3x+3 cắt nhau tại một điểm trên trục tung nên giao điểm của (d′):y=3x+3 với trục tung cũng nằm trên (d)y=(m+2)x+2m2+1.
Thay tọa độ giao điểm vừa tìm được vào đường thẳng (d)y=(m+2)x+2m2+1 để tìm m.
Lời giải chi tiết:
Cho hàm số y=(m+2)x+2m2+1 (m là tham số)
a) Vẽ đồ thị hàm số trên khi m=−1.
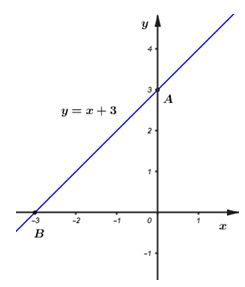
Với m=−1 ta có hàm số có dạng:y=x+3
Chọn x=0⇒y=3⇒A(0;3) thuộc đồ thị hàm số
Chọn y=0⇒x+3=0⇔x=−3⇒B(−3;0) thuộc đồ thị hàm số.
Từ đó ta có đồ thị hàm số:
b) Tìm m để hai đường thẳng (d)y=(m+2)x+2m2+1và (d′):y=3x+3 cắt nhau tại một điểm trên trục tung.
Phương trình của trục tung có dạng x=0. Thay x=0 vào hàm số (d′):y=3x+3 ta có y=3
Suy ra A(0;3) là giao điểm của(d′):y=3x+3 và trục tung.
Vì hai đường thẳng (d):y=(m+2)x+2m2+1và (d′):y=3x+3 cắt nhau tại một điểm trên trục tung nên điểm A(0;3) thuộc đường thẳng (d):y=(m+2)x+2m2+1
⇒3=(m+2).0+2m2+1⇔m2=1⇔m=±1.
Với m=1⇒y=3x+3⇒(d) trùng với (d′):y=3x+3 (loại vì nếu hai đường thẳng trùng nhau thì không thể cắt nhau tại 1 điểm)
Với m=−1⇒y=x+3 (thỏa mãn)
Vậym=−1 là giá trị cần tìm.
Chọn đáp án B.