Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho hàm số \(y = (2m + 1)x - 6\) có đồ thị \((d)\).
a) Với giá trị nào của \(m\) thì hàm số nghịch biến trên \(R\).
b) Tìm \(m\) để đồ thị hàm số \((d)\) đã cho đi qua điểm \(A(1;\,\,2)\).
c) Vẽ \((d)\) khi \(m = - 2\).
- A \(\begin{array}{l}a)\,\,m > \frac{{ - 1}}{2}\\b)\,\,m = \frac{5}{2}\end{array}\)
- B \(\begin{array}{l}a)\,\,m < \frac{{ - 1}}{2}\\b)\,\,m = \frac{7}{2}\end{array}\)
- C \(\begin{array}{l}a)\,\,m < \frac{1}{2}\\b)\,\,m = \frac{{ - 7}}{2}\end{array}\)
- D \(\begin{array}{l}a)\,\,m > \frac{1}{2}\\b)\,\,m = \frac{{ - 5}}{2}\end{array}\)
Phương pháp giải:
a) Hàm số \(y = ax + b\) nghịch biến \( \Leftrightarrow a < 0.\)
b) Thay tọa độ điểm \(A\left( {1;\;2} \right)\) vào công thức của đường thẳng \(\left( d \right)\) để tìm \(m.\)
c) Thay giá trị \(m = - 2\) vào công thức của đường thẳng \(\left( d \right)\) sau đó vẽ đồ thị hàm số bậc nhất.
Lời giải chi tiết:
a) Hàm số bậc nhất \(y = (2m + 1)x - 6\) nghịch biến trên \(R\) khi \(2m + 1 < 0\)
\( \Leftrightarrow 2m < - 1\,\, \Leftrightarrow m < \frac{{ - 1}}{2}\)
b) Đồ thị hàm số \(y = (2m + 1)x - 6\) đi qua điểm \(A(1\,;\,\,2)\,\,\)
\(\begin{array}{l} \Leftrightarrow 2 = (2m + 1).1 - 6\\ \Leftrightarrow 2 = 2m + 1 - 6\,\,\\ \Leftrightarrow 2m = 7\,\,\\ \Leftrightarrow m = \frac{7}{2}.\end{array}\)
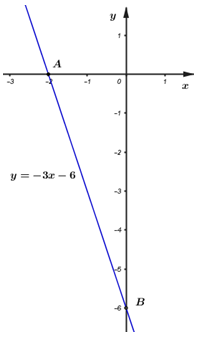
c) Khi \(m = - 2\) ta có \(y = - 3x - 6\).
Cho \(x = 0 \Rightarrow y = - 6\,;\,\,\,\,\,\,\,\,\,y = 0 \Rightarrow x = - 2\)
Đồ thị hàm số \(y = - 3x - 6\) đi qua \(2\) điểm \(A\,( - 2\,;\,\,0);\,\,B\,(0\,;\,\, - 6)\)
Chọn B.