Nội dung từ Loigiaihay.Com
Câu hỏi:
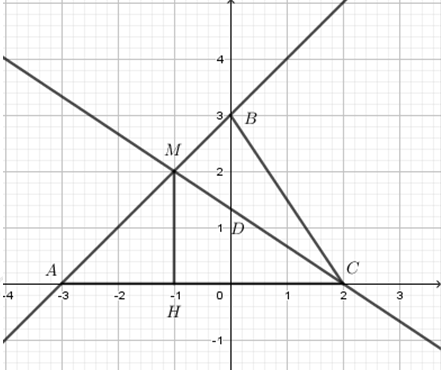
Cho 2 đường thẳng d:y=x+3;d′:y=−23x+43. Gọi M là giao điểm của d và d′ . A và C lần lượt là giao điểm của d và d′ với trục hoành; B và D lần lượt là giao điểm của d và d′ với trục tung. Khi đó diện tích tam giác CMB là:
- A 5 (đvdt)
- B 52 (đvdt)
- C 54(đvdt)
- D 10(đvdt)
Phương pháp giải:
Phương pháp:
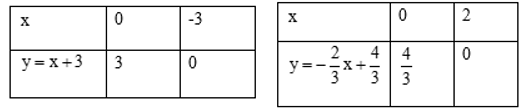
- Lập bảng giá trị để xác định 2 điểm thuộc đường thẳng.
- Xác định giao điểm 2 đường thẳng đã cho
- Tính độ dài các đoạn thẳng cần thiết
- Dựng đường cao của tam giác được tạo thành
- Tính diện tích các tam giác phụ được tạo thành
- Tính diện tích tam giác theo yêu cầu đề bài
Lời giải chi tiết:
Cách giải:
Xét phương trình hoành độ giao điểm:
x+3=−23x+43⇔3x+9=−2x+4⇔5x=−5⇔x=−1⇒y=2
Do đó giao điểm của 2 đường thẳng đã cho là M(−1;2)
d∩Ox=A(−3;0)⇒OA=3d′∩Ox=C(2;0)⇒OC=2d∩Oy=B(0;3)⇒OB=3d′∩Oy=D(0;43)⇒AC=OA+OC=3+2=5SΔABC=12AC.OB=12.5.3=152(dvdt)
Gọi H là hình chiếu của M trên Ox
⇒MH=|yM|=2SΔAMC=12MH.AC=12.2.5=5(dvdt)SΔBMC=SΔABC−SΔAMC=152−5=52(dvdt)
Chọn B.