Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho đường thẳng \(d:y=x+2;d':y=-2x+5\). Gọi \(M\) là giao điểm của \(d\) và \(d'\) . \(A\) và \(B\) lần lượt là giao điểm của \(d\) và \(d'\) với trục hoành. Khi đó diện tích tam giác \(AMB\) là:
- A \(\frac{27}{6}\)\(\)( đvdt)
- B \(27\)( đvdt)
- C \(\frac{27}{2}\) (đvdt)
- D \(\frac{27}{4}\)(đvdt)
Phương pháp giải:
Phương pháp:
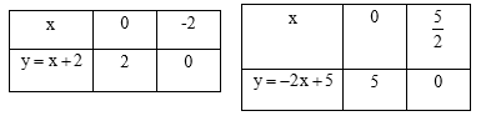
- Lập bảng giá trị để xác định 2 điểm thuộc đường thẳng.
- Xác định giao điểm 2 đường thẳng đã cho
- Dựng đường cao của tam giác được tạo thành
- Tính độ dài các đoạn thẳng
- Tính diện tích tam giác
Lời giải chi tiết:
Cách giải:
Xét phương trình hoành độ giao điểm của \({{d}_{1}};{{d}_{2}}\)
\(x+2=-2x+5\Leftrightarrow x=1\Rightarrow y=3\Rightarrow {{d}_{1}}\cap {{d}_{2}}=M(1;3)\)
Gọi \(H\) là chân đường vuông góc kẻ từ \(M\) tới \(Ox\). Suy ra \(MH=3\)
\(\begin{align}& d\cap Ox=A(-2;0)\Rightarrow OA=2 \\ & d'\cap Ox=B\left( \frac{5}{2};0 \right)\Rightarrow OB=\frac{5}{2} \\ & \Rightarrow AB=2+\frac{5}{2}=\frac{9}{2} \\\end{align}\)
\({{S}_{MAB}}=\frac{1}{2}AB.MH=\frac{1}{2}.\frac{9}{2}.3=\frac{27}{4}(dvdt)\)
Chọn D.