Nội dung từ Loigiaihay.Com
Câu hỏi:
Chóp S.ABC, \(SA \bot \left( {ABC} \right),\,\,\Delta ABC\) vuông ở A. \(AB = a,\,\,AC = a\sqrt 2 ;\,\,{S_{\Delta SBC}} = \dfrac{{{a^2}\sqrt {33} }}{6}\). M là trung điểm AB. Tính \(d\left( {M;\left( {SBC} \right)} \right)\).
- A \(\dfrac{{a\sqrt {330} }}{{66}}\)
- B \(\dfrac{{a\sqrt {33} }}{{66}}\)
- C \(\dfrac{{a\sqrt {336} }}{{66}}\)
- D \(\dfrac{{a\sqrt {30} }}{{66}}\)
Phương pháp giải:
Lời giải chi tiết:
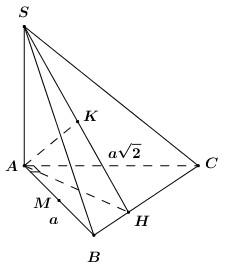
Kẻ \(AH \bot BC\) ta có: \(\left\{ \begin{array}{l}BC \bot AH\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAH} \right)\).
Trong \(\left( {SAH} \right)\) kẻ \(AK \bot SH\) \( \Rightarrow BC \bot AK\).
Do đó \(AK \bot \left( {SBC} \right) \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AK\).
Ta có: \(AM \cap \left( {SBC} \right) = B \Rightarrow \frac{{d\left( {A;\left( {SBC} \right)} \right)}}{{d\left( {M;\left( {SBC} \right)} \right)}} = \frac{{AB}}{{MB}} = 2\).
\( \Rightarrow d\left( {M;\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = \frac{1}{2}AK\).
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{2{a^2}}} = \frac{3}{{2{a^2}}} \Rightarrow AH = \frac{{a\sqrt 6 }}{3}\).
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 \).
\({S_{\Delta SBC}} = \frac{1}{2}SH.BC \Rightarrow SH = \frac{{2{S_{\Delta SBC}}}}{{BC}} = \frac{{2.\frac{{{a^2}\sqrt {33} }}{6}}}{{a\sqrt 3 }} = \frac{{a\sqrt {11} }}{3}\).
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AH \Rightarrow \Delta SAH\) vuông tại \(A\).
\( \Rightarrow SA = \sqrt {S{H^2} - A{H^2}} = \sqrt {\frac{{11{a^2}}}{9} - \frac{{2{a^2}}}{3}} = \frac{{a\sqrt 5 }}{3}\).
Áp dụng hệ thức lượng trong tam giác vuông \(SAH\) có: \(AK = \frac{{SA.AH}}{{SH}} = \frac{{\frac{{a\sqrt 5 }}{3}.\frac{{a\sqrt 6 }}{3}}}{{\frac{{a\sqrt {11} }}{3}}} = \frac{{a\sqrt {30} }}{{3\sqrt {11} }}\).
Vậy \(d\left( {M;\left( {SBC} \right)} \right) = \frac{{a\sqrt {30} }}{{6\sqrt {11} }} = \frac{{a\sqrt {330} }}{{66}}\).
Chọn A.













