Nội dung từ Loigiaihay.Com
Câu hỏi:
Hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(SA = SB = SC = a\), \(\angle SAB = {30^0}\), \(\angle SBC = {60^0}\), \(\angle SCA = {45^0}\). Tính khoảng cách d giữa 2 đường thẳng \(AB\) và \(SD\)?
- A \(\dfrac{{4a\sqrt {11} }}{{11}}\)
- B \(\dfrac{{a\sqrt {22} }}{{22}}\)
- C \(\dfrac{{a\sqrt {22} }}{{11}}\)
- D \(\dfrac{{2a\sqrt {22} }}{{11}}\)
Phương pháp giải:
- Chuyển tính khoảng cách từ hai đường thẳng chéo nhau sang tính khoảng cách từ điểm đến mặt phẳng.
- Nhận dạng tam giác ABC, tìm vị trí tâm đường tròn ngoại tiếp tam giác này, từ đó suy ra đường cao của hình chóp S.ABCD.
Lời giải chi tiết:
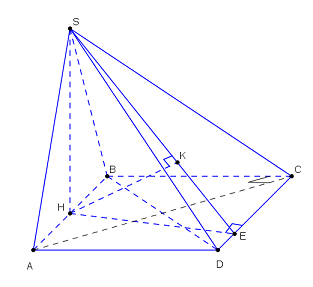
\(\begin{array}{l}S{B^2} = S{A^2} + A{B^2} - 2.SA.AB.\cos {30^0}\\ \Leftrightarrow {a^2} = {a^2} + A{B^2} - 2.a.AB.\dfrac{{\sqrt 3 }}{2}\\ \Leftrightarrow A{B^2} - AB.a\sqrt 3 = 0 \Leftrightarrow AB = a\sqrt 3 \end{array}\)
\(BC = SB = SC = a\) (Tam giác SBC đều)
\(\begin{array}{l}S{A^2} = S{C^2} + A{C^2} - 2.SA.AC.\cos {45^0}\\ \Leftrightarrow {a^2} = {a^2} + A{C^2} - 2.a.AC.\dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow A{C^2} - AC.a\sqrt 2 = 0 \Leftrightarrow AC = a\sqrt 2 \end{array}\)
\( \Rightarrow \) Tam giác ABC vuông tại C
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC \( \Rightarrow H\) là trung điểm của AB và \(SH \bot \left( {ABCD} \right)\).
Tam giác SAH vuông tại H \( \Rightarrow SH = SA.\sin \widehat {SAB} = a.\sin {30^0} = \dfrac{a}{2}\)
Kẻ \(HE \bot CD,\,HK \bot SE \Rightarrow HK \bot \left( {SCD} \right)\). Ta có: \(AB\parallel \left( {SCD} \right)\)
\( \Rightarrow d\left( {AB;CD} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {H;\left( {SCD} \right)} \right) = HK\)
Ta có: \({S_{ABCD}} = 2.{S_{ABC}} = 2.\dfrac{1}{2}.BC.AC = a.a\sqrt 2 = {a^2}\sqrt 2 \)
Lại có: \({S_{ABCD}} = HE.DC = HE.AB = HE.a\sqrt 3 = {a^2}\sqrt 2 \Rightarrow HE = \dfrac{{a\sqrt 6 }}{3}\)
Tam giác SHE vuông tại H, HK là đường cao
\( \Rightarrow \dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{E^2}}} = \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {\dfrac{{a\sqrt 6 }}{3}} \right)}^2}}} = \dfrac{4}{{{a^2}}} + \dfrac{3}{{2{a^2}}} = \dfrac{{11}}{{2{a^2}}}\)
\( \Rightarrow HK = \dfrac{{a\sqrt {22} }}{{11}} \Rightarrow d\left( {AB;SD} \right) = \dfrac{{a\sqrt {22} }}{{11}}\)
Chọn C.













