Nội dung từ Loigiaihay.Com
Câu hỏi:
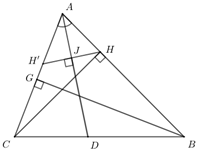
Cho tam giác ABCcó phương trình đường phân giác trong góc A, đường cao kẻ từ B lần lượt là x−y+2=0, 4x+3y−1=0. Biết hình chiếu vuông góc của C lên đường thẳng AB là H(−1;−1). Tọa độ đỉnh A là:
- A A(7;−5)
- B A(7;5)
- C A(−5;7)
- D A(5;7)
Phương pháp giải:
+) Lấy điểm H′ là điểm đối xứng với H qua AD⇒ Xác định được tọa độ H′
+) Viết phương trình đường thẳng AC
+) A là giao điểm của AC và AD
Lời giải chi tiết:
*) Phương trình đường phân giác AD: x−y+2=0⇒→nAD=(1;−1)⇒→uAD=(1;1)
*) Gọi H′ là điểm đối xứng với H qua AD⇒HH′⊥AD
+) Phương trình đường thẳng HH′ đi qua H(−1;−1) nhận →uAD=(1;1) là VTPT:
HH′:x+1+y+1=0⇔x+y+2=0
+) Gọi J=HH′∩AD. Tọa độ của điểm J là nghiệm của hệ phương trình:
{x+y+2=0x−y+2=0⇒{x=−2y=0⇒J(−2;0)
+) J là trung điểm của HH′. Tọa độ của H′là {xH′=2.(−2)−(−1)yH′=2.0−(−1)⇒{xH′=−3yH′=1⇒H′(−3;1)
*) Phương trình đường cao BG: 4x+3y−1=0⇒→nBG=(4;3)⇒→uBG=(3;−4)
*) Viết phương trình đường thẳng AC
Vì BG⊥AC tại G nên phương trình đường thẳng AC đi qua H′(−3;1) nhận →uBG=(3;−4) là VTPT là:
AC:3.(x+3)+(−4).(y−1)=0⇔3x+9−4y+4=0⇔3x−4y+13=0
*) Xác định tọa độ điểm A
Phương trình đường phân giác AD là: x−y+2=0
Phương trình đường thẳng AC là: 3x−4y+13=0
Vì AC∩AD=A nên tọa độ điểm A là nghiệm của hệ phương trình:
{3x−4y+13=0x−y+2=0⇒{x=5y=7⇒A(5;7)
Vậy A(5;7).
Chọn D.