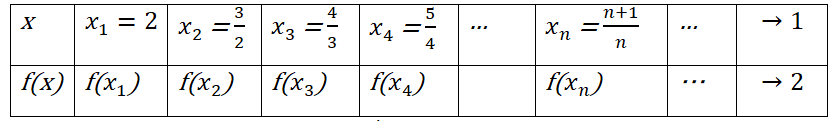Câu hỏi 1 trang 123 SGK Đại số và Giải tích 11

LG 1

Cho biến \(x\) những giá trị khác 1 lập thành dãy số \({x_n},{\rm{ }}{x_n}\; \to {\rm{ }}1\) như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số

\(f({x_1}),{\rm{ }}f({x_2}), \ldots ,{\rm{ }}f({x_n}),{\rm{ }} \ldots \)

cũng lập thành một dãy số mà ta kí hiệu là \((f({x_n})).\)

a) Chứng minh rằng \(f\left( {{x_n}} \right) = 2{x_n} = \dfrac{{2n + 2}}{n}\)

b) Tìm giới hạn của dãy số \((f({x_n})).\)

Phương pháp giải:

a) Tính và rút gọn \(f\left( {{x_n}} \right)\) suy ra đáp số, chú ý \(x_n=\dfrac{{n + 1}}{n}\).

b) Xét giới hạn \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2)\) và suy ra đáp số.

Lời giải chi tiết:

a) \(\displaystyle f({x_n}) = {{2{x_n}^2 - 2{x_n}} \over {{x_n} - 1}} = {{2{x_n}({x_n} - 1)} \over {{x_n} - 1}} \) \(= 2{x_n}\)

\(\displaystyle {x_n} = {{n+1} \over {n}} \) \(\displaystyle \Rightarrow f({x_n}) = 2{x_n} = 2.{{n+1} \over {n}} = {{2n+2} \over {n}}\)

b) \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2) \) \(\displaystyle = \mathop {\lim }\limits_{n \to + \infty } ({{2n+2} \over {n}} - 2) = \mathop {\lim }\limits_{n \to + \infty } {{ 2} \over {n}}\)

Ta có: \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } {{ 2} \over {n}} = 0 \) \(\displaystyle \Rightarrow \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2) = 0 \) \(\displaystyle \Rightarrow \mathop {\lim }\limits_{n \to + \infty } f({x_n}) = 2\)

LG 2

Chứng minh rằng với dãy số bất kì \({x_n},{\rm{ }}{x_n}\; \ne {\rm{ }}1\) và \({x_n}\; \to {\rm{ }}1\), ta luôn có \(\;f({x_n}) \to 2.\)

(Với tính chất thể hiện trong câu 2, ta nói hàm số \(\displaystyle f(x) = {{2{x^2} - 2x} \over {x - 1}}\) có giới hạn là 2 khi \(x\) dần tới 1).

Phương pháp giải:

Tính \(\lim f({x_n})\) dựa vào công thức có được ở phần 1a.

Lời giải chi tiết:

\(\lim f({x_n}) = \lim\,2{x_n} \) \(= 2\lim {x_n} = 2.1 = 2\)

 HocTot.Nam.Name.Vn