Bài 1.47 trang 19 SBT Giải tích 12 Nâng cao

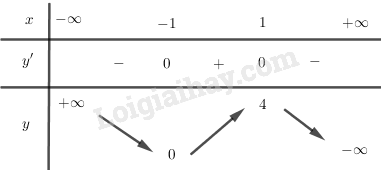
LG a

Tìm các hệ số m, n sao cho hàm số

$y =  - {x^3} + mx + n$

Đạt cực tiểu tại điểm x = -1 và đồ thị của nó đi qua điểm (1;4).

Lời giải chi tiết:

Ta có:

$\begin{array}{l}f'\left( x \right) =  - 3{x^2} + m\\f''\left( x \right) =  - 6x\end{array}$

Hàm số đạt cực tiểu tại $x =  - 1$

$\Leftrightarrow \left\{ \begin{array}{l}f'\left( { - 1} \right) = 0\\f''\left( { - 1} \right) > 0\end{array} \right.$

$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - 3.{\left( { - 1} \right)^2} + m = 0\\ - 6.\left( { - 1} \right) > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m - 3 = 0\\6 > 0\left( {dung} \right)\end{array} \right.\\ \Leftrightarrow m = 3\end{array}$

Do đó $f\left( x \right) =  - {x^3} + 3x + n$.

Đồ thị đi qua $\left( {1;4} \right)$ $\Leftrightarrow f\left( 1 \right) = 4$

$\Leftrightarrow  - {1^3} + 3.1 + n = 4$  

$\Leftrightarrow 2 + n = 4 \Leftrightarrow n = 2$

Vậy $m = 3,n = 2$.

LG b

Khảo sát sự biến thiên và vẽ đồ thị của hàm số với các giá trị m, n vừa tìm được.

Lời giải chi tiết:

Với $m = 3,n = 2$ ta có $y =  - {x^3} + 3x + 2$

+) TXĐ: $D = \mathbb{R}$.

+) Chiều biến thiên:

$\mathop {\lim }\limits_{x \to  + \infty } y =  - \infty ,\mathop {\lim }\limits_{x \to  - \infty } y =  + \infty$

$\begin{array}{l}y' =  - 3{x^2} + 3\\y' = 0 \Leftrightarrow  - 3{x^2} + 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 1\end{array} \right.\end{array}$

BBT:

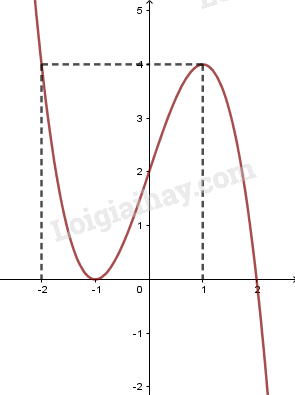
Hàm số nghịch biến trên $\left( { - \infty ; - 1} \right)$ và $\left( {1; + \infty } \right)$.

Hàm số đồng biến trên $\left( { - 1;1} \right)$.

Hàm số đạt cực đại tại $x = 1,{y_{CD}} = 4$

Hàm số đạt cực tiểu tại $x =  - 1,{y_{CT}} = 0$.

+) Đồ thị:

$\begin{array}{l}y'' =  - 6x\\y'' = 0 \Leftrightarrow  - 6x = 0\\ \Leftrightarrow x = 0 \Rightarrow y\left( 0 \right) = 2\end{array}$

Điểm uốn $I\left( {0;2} \right)$.

Đồ thị hàm số cắt trục tung tại điểm $\left( {0;2} \right)$, đi qua điểm $\left( { - 2;4} \right)$.

Điểm cực đại $\left( {1;4} \right)$ và điểm cực tiểu $\left( { - 1;0} \right)$.

Phương trình hoành độ giao điểm:

$\begin{array}{l} - {x^3} + 3x + 2 = 0\\ \Leftrightarrow {x^3} - 3x - 2 = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2}\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 2\end{array} \right.\end{array}$

Đồ thị cắt trục hoành tại điểm $\left( {2;0} \right)$ và tiếp xúc trục hoành tại điểm $\left( { - 1;0} \right)$.

HocTot.Nam.Name.Vn