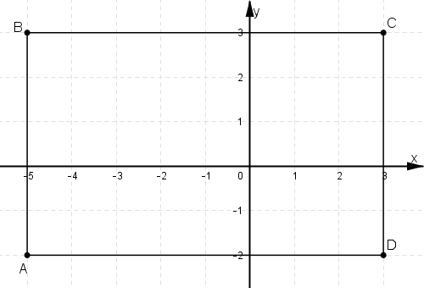
Bài 13 trang 30 SGK Hình học 10

Đề bài

Trong mặt phẳng \(Oxy\) cho bốn điểm \(A(-5; -2); B(-5; 3); C(3; 3); D(3; -2)\).

Khẳng định nào sau đây là đúng?

A. \(\overrightarrow {AB} ;\overrightarrow {CD} \) cùng hướng

B. Tứ giác ABCD là hình chữ nhật

C. Điểm \(I(-1; 1)\) là trung điểm của \(AC\)

D. \(\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OC} \)

Lời giải chi tiết

Trắc nghiệm:

Từ hình vẽ ta thấy ABCD là hình chữ nhật.

Chọn B.

Tự luận:

Ta có:

\(\begin{array}{l}
\overrightarrow {AB} = \left( { - 5 + 5;3 + 2} \right) = \left( {0;5} \right)\\
\overrightarrow {DC} = \left( {3 - 3;3 + 2} \right) = \left( {0;5} \right)\\
\Rightarrow \overrightarrow {AB} = \overrightarrow {DC}
\end{array}\)

Mà \(\overrightarrow {AD}  = \left( {3 + 5; - 2 + 2} \right) = \left( {8;0} \right)\) nên \(\overrightarrow {AB} ,\overrightarrow {AD} \) không cùng phương.

Do đó ABCD là hình bình hành.

Mà \(\overrightarrow {AB}  = 5\overrightarrow j \) nên cùng phương với \(\overrightarrow j \).

\(\overrightarrow {AD}  = 8\overrightarrow i \) nên cùng phương với \(\overrightarrow i \)

Lại có \(\overrightarrow i \) và \(\overrightarrow j \) có phương vuông góc nhau nên AB vuông góc AD.

Vậy ABCD là hình chữ nhật.

Do đó chọn B.

Ngoài ra, A sai vì \(\overrightarrow {AB} ;\overrightarrow {CD} \) ngược hướng.

C sai vì trung điểm AC có tọa độ \(\left( { - 1;\frac{1}{2}} \right)\)

D sai vì:

\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} = \left( { - 5 - 5; - 2 + 3} \right) = \left( { - 10;1} \right)\\
\overrightarrow {OC} = \left( {3;3} \right)\\
\Rightarrow \overrightarrow {OA} + \overrightarrow {OB} \ne \overrightarrow {OC}
\end{array}\)

HocTot.Nam.Name.Vn