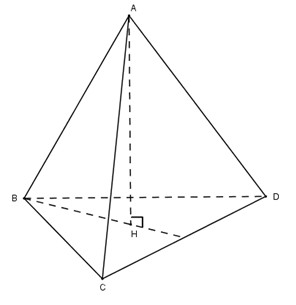
Giải bài 1 trang 25 SGK Hình học 12Tính thể tích khối tứ diện đều cạnh a. Đề bài Tính thể tích khối tứ diện đều cạnh aa. Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Gọi AHAH là đường cao hạ từ đỉnh AA của tứ diện đều ABCDABCD (H∈(BCD))(H∈(BCD)). +) Do tứ diện ABCDABCD đều, chứng minh HH là trọng tâm tam giác ABCABC. +) Sử dụng định lí Pytago tính độ dài AHAH. +) Áp dụng công thức tính thể tích: VABCD=13AH.SBCDVABCD=13AH.SBCD. Lời giải chi tiết
Cho tứ diện đều ABCDABCD. Hạ AH⊥(BCD)AH⊥(BCD) Dễ dàng chứng minh được ΔvAHB=ΔvAHC=ΔvAHD(ch−cgv)ΔvAHB=ΔvAHC=ΔvAHD(ch−cgv) ⇒HB=HC=HD,⇒HB=HC=HD, do đó H là tâm đường tròn ngoại tiếp tam giác BCDBCD. Do BCDBCD là tam giác đều nên HH là trọng tâm của tam giác BCDBCD. Gọi MM là trung điểm CDCD thì BMBM vừa là trung tuyến vừa là đường cao trong tam giác. Ta có: BM=BDsin600=a√32BM=BDsin600=a√32 Do đó BH=23BM=23.√32a=√33aBH=23BM=23.√32a=√33a Áp dụng định lí Pitago trong tam giác vuông ABHABH ta có: AH2=AB2−BH2=a2−a23=2a23AH2=AB2−BH2=a2−a23=2a23 ⇒AH=a√63⇒AH=a√63 Do tam giác BCDBCD đều cạnh aa nên: SBCD=a2√34SBCD=a2√34 Vậy VABCD=13AH.SBCDVABCD=13AH.SBCD =13.a√63.a2√34=13.a√63.a2√34 =a3√212.=a3√212. HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|