Nội dung Tổng hợp
Cho nửa đường tròn (O) , đường kính AB và một dây MN . Kẻ AE và BF vuông góc với MN lần lượt tại E và F . So sánh độ dài OE và OF .
-
A.
OE=OF
-
B.
OE=32OF
-
C.
OE<OF
-
D.
OE>OF
Bước 1: Lấy I là trung điểm của EF
Bước 2: Sử dụng mối liên hệ giữa đường kính và dây của đường tròn để hoàn thành.

Lấy I là trung điểm của EF
Xét tứ giác AEFB có AE//FB (vì cùng vuông với EF) nên AEFB là hình thang vuông tại E;F.
Ta có OI là đường trung bình của hình thang AEFB nên OI//AE//FB⇒OI⊥EF
Hay OI⊥CD nên I là trung điểm của CD ( quan hệ giữa dây và đường kính)
Xét tam giác OEF có OI vừa là đường cao vừa là đường trung tuyến nên ΔOEF cân tại O
Suy ra OE=OF.
Đáp án : A

Các bài tập cùng chuyên đề
Bài 1 :
Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?
-
A.
AB>CD
-
B.
AB=CD
-
C.
AB<CD
-
D.
AB≤CD
Bài 2 :
Cho đường tròn (O) có hai dây AB,CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng?
-
A.
AB>CD
-
B.
AB=CD
-
C.
AB<CD
-
D.
AB//CD
Bài 3 :
“Trong một đường tròn, đường kính đi qua trung điểm một dây không đi qua tâm thì …với dây ấy”. Điền vào dấu ... cụm từ thích hợp.
-
A.
nhỏ hơn
-
B.
bằng
-
C.
song song
-
D.
vuông góc
Bài 4 :
Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn
-
A.
Dây nào lớn hơn thì dây đó xa tâm hơn
-
B.
Dây nào nhỏ hơn thì dây đó xa tâm hơn
-
C.
Dây nào gần tâm hơn thì dây đó lớn hơn
-
D.
Hai dây bằng nhau thì cách đều tâm
Bài 5 :
Cho đường tròn (O) có bán kính R=5cm. Khoảng cách từ tâm đến dây AB là 3cm. Tính độ dài dây AB.
-
A.
AB=6cm
-
B.
AB=8cm
-
C.
AB=10cm
-
D.
AB=12cm
Bài 6 :
Cho đường tròn (O;R)có hai dây AB,CD bằng nhau và vuông góc với nhau tại I. Giả sử IA=2cm;IB=4cm . Tổng khoảng cách từ tâm O dây AB,CD là
-
A.
4cm
-
B.
1cm
-
C.
3cm
-
D.
2cm
Bài 7 :
Cho đường tròn (O;R)có hai dây AB,CD vuông góc với nhau ở M. BiếtAB=16cm;CD=12cm;MC=2cm. Khoảng cách từ tâm O đến dây AB là
-
A.
4cm
-
B.
5cm
-
C.
3cm
-
D.
2cm
Bài 8 :
Cho đường tròn (O;R) có hai dây AB,CD vuông góc với nhau ở M. Biết AB=14cm;CD=12cm;MC=2cm. Bán kính R và khoảng cách từ tâm O đến dây CD lần lượt là
-
A.
8cm;√29cm
-
B.
√65cm;√29cm
-
C.
√29cm;√65cm
-
D.
√29cm;8cm
Bài 9 :
Cho nửa đường tròn (O), đường kính AB và một dây CD. Kẻ AE và BF vuông góc với CD lần lượt tại E và F . So sánh độ dài CE và DF .
-
A.
CE>DF
-
B.
CE=2DF
-
C.
CE<DF
-
D.
CE=DF
Bài 10 :
Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. So sánh độ dài AC và BD .
-
A.
AC>BD
-
B.
AC<BD
-
C.
AC=BD
-
D.
AC=3BD
Bài 11 :
Cho đường tròn (O), dây cung AB và CD với CD<AB. Giao điểm K của các đường thẳng AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O;OK), đường tròn này cắt KA và KC lần lượt tại M và N . So sánh KM và KN.
-
A.
KN>KM
-
B.
KN<KM
-
C.
KM=KN
-
D.
KN=43KM
Bài 12 :
Cho đường tròn (O;10cm). Dây AB và CD song song, có độ dài lần lượt là 16cm và 12cm .Tính khoảng cách giữa hai dây.
-
A.
14cm
-
B.
10cm
-
C.
12cm
-
D.
16cm
Bài 13 :
Cho tam giác ABC nhọn và có các đường cao BD,CE. So sánh BC và DE .
-
A.
BC=DE
-
B.
BC<DE
-
C.
BC>DE
-
D.
BC=23DE
Bài 14 :
Cho đường tròn (O) đường kính AB=14cm, dây CD có độ dài 12cm vuông góc với AB tại H nằm giữa O và B. Độ dài HA là
-
A.
7+√13cm
-
B.
7−√13cm
-
C.
7cm
-
D.
7−2√13cm
Bài 15 :
Phát biểu nào sau đây là sai:
-
A.
Đường kính đi qua trung điểm dây cung thì vuông góc với dây ấy
-
B.
Đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy
-
C.
Đường kính đi qua trung điểm của một dây(dây không đi qua tâm) thì vuông góc với dây ấy
-
D.
Đường kính vuông góc với một dây thì hai đầu mút của dây ấy đối xứng qua đường kính này
Bài 16 :
Trong hình vẽ bên cho OC⊥AB,AB=12cm,OA=10cm. Độ dài AC là:
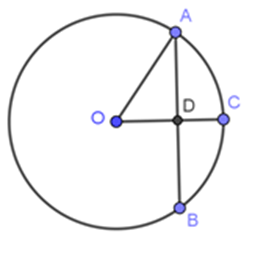
-
A.
8cm
-
B.
2√10cm
-
C.
4√7cm
-
D.
2cm
Bài 17 :
Cho đường tròn (O;25cm) và dây AB bằng 40cm. Khi đó khoảng cách từ tâm O đến dây AB là
-
A.
15cm
-
B.
7cm
-
C.
20cm
-
D.
24cm
Bài 18 :
“Trong các dây của một đường tròn, đường kính là dây có độ dài…”. Cụm từ thích hợp điền vào chỗ trống là:
-
A.
nhỏ nhất
-
B.
lớn nhất
-
C.
bằng 10cm
-
D.
bằng tổng hai dây bất kỳ
Bài 19 :
Cho đường tròn (O)có hai dây AB,CD không đi qua tâm. Biết rằng khoảng cách từ tâm O đến dây AB lớn hơn khoảng cách từ tâm O đến dây CD. Kết luận nào sau đây là đúng?
-
A.
AB>CD
-
B.
AB=CD
-
C.
AB<CD
-
D.
AB//CD
Bài 20 :
“Trong một đường tròn, đường kính vuông góc với dây thì …của dây ấy”. Điền vào dấu ... cụm từ thích hợp.
-
A.
đi qua trung điểm
-
B.
đi qua giao điểm của dây ấy với đường tròn
-
C.
đi qua điểm bất kì
-
D.
đi qua điểm chia dây ấy thành hai phần có tỉ lệ 2:3
Bài 21 :
Chọn khẳng định đúng trong các khẳng định sau. Trong hai dây của một đường tròn
-
A.
Dây nào lớn hơn thì dây đó xa tâm hơn
-
B.
Hai dây đi qua tâm thì vuông góc với nhau
-
C.
Dây nào gần tâm hơn thì dây đó nhỏ hơn
-
D.
Hai dây cách đều tâm thì bằng nhau
Bài 22 :
Cho đường tròn (O) có bán kính R=6,5cm. Khoảng cách từ tâm đến dây AB là 2,5cm. Tính độ dài dây AB.
-
A.
AB=6cm
-
B.
AB=8cm
-
C.
AB=10cm
-
D.
AB=12cm
Bài 23 :
Cho đường tròn (O;R) có hai dây AB,CD bằng nhau và vuông góc với nhau tại I . Giả sử IA=6cm;IB=3cm . Tổng khoảng cách từ tâm O dây AB,CD là
-
A.
4cm
-
B.
1cm
-
C.
3cm
-
D.
2cm
Bài 24 :
Cho đường tròn (O;R) có hai dây AB,CD vuông góc với nhau ở M. BiếtCD=8cm;MC=1cm. Khoảng cách từ tâm O đến dây AB là
-
A.
4cm
-
B.
5cm
-
C.
3cm
-
D.
2cm
Bài 25 :
Cho đường tròn (O;R)có hai dây AB,CD vuông góc với nhau ở M. BiếtAB=10cm;CD=8cm;MC=1cm. Bán kính R và khoảng cách từ tâm O đến dây CD lần lượt là
-
A.
√34cm;9cm
-
B.
6cm;3cm
-
C.
√34cm;3√2cm
-
D.
3√2cm;√34cm
Bài 26 :
Cho đường tròn (O) , đường kính AB . Lấy điểm C là trung điểm đoạn OB. Kẻ dây MN qua C và dây AD//MN. So sánh độ dài AD và MN .
-
A.
AD=2.MN
-
B.
AD=MN
-
C.
AD>MN
-
D.
AD<MN
Bài 27 :
Cho đường tròn (O), dây cung AB và CD với CD=AB. Giao điểm K của các đường thẳng AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O;OK), đường tròn này cắt KA và KC lần lượt tại M và N . So sánh KM và KN.
-
A.
KN>KM
-
B.
KN<KM
-
C.
KM=KN
-
D.
KN=43KM
Bài 28 :
Cho đường tròn (O;8cm). Dây AB và CD song song, có độ dài lần lượt là 14cm và 10cm .Tính khoảng cách giữa hai dây.
-
A.
2√15(cm)
-
B.
2√39(cm)
-
C.
√39+√152(cm)
-
D.
√39+√15(cm)
Bài 29 :
Cho hình vuông ABCD. Gọi M,N lần lượt là trung điểm của AB,BC . Gọi E là giao điểm của CM và DN . So sánh AE và DM.
-
A.
AM=32AE
-
B.
DM<AE
-
C.
DM=AE
-
D.
DM>AE
Bài 30 :
Cho đường tròn (O) đường kính AB=20cm , dây CD có độ dài 16cm vuông góc với AB tại H nằm giữa O và B. Độ dài HA là
-
A.
12cm
-
B.
18cm
-
C.
16cm
-
D.
15cm












