Nội dung từ Loigiaihay.Com
Cho \(\Delta ABC\) vuông tại $A.$ Trên cạnh $AB$ và $AC$ lấy tương ứng hai điểm $D$ và $E$ ($D,E$ không trùng với các đỉnh của \(\Delta ABC\)). Chọn đáp án đúng nhất.
-
A.
\(DE > BE > BC\)
-
B.
\(DE < BE < BC\)
-
C.
\(DE > BE = BC\)
-
D.
\(DE < BE = BC\)
+ Góc tù là góc lớn nhất trong tam giác
+ Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất
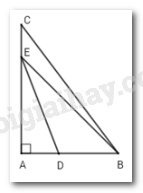
Ta có: Góc EDB là góc ngoài tại đỉnh D của tam giác ADE nên \(\widehat {EDB} > \widehat {DAE} = 90^\circ \Rightarrow \widehat {EDB}\) là góc tù.
Góc BEC là góc ngoài tại đỉnh E của tam giác ABE nên \(\widehat {BEC} > \widehat {BAE}\)( định lí) \( \Rightarrow \widehat {BEC}\) là góc tù.
Xét tam giác BDE có góc BDE là góc tù nên là góc lớn nhất trong tam giác. Cạnh EB đối diện với góc BDE nên là cạnh lớn nhất trong tam giác. Ta được DE < EB.(1)
Xét tam giác BEC có góc BEC là góc tù nên là góc lớn nhất trong tam giác. Cạnh CB đối diện với góc BEC nên là cạnh lớn nhất trong tam giác. Ta được EB < CB.(2)
Từ (1) và (2) \( \Rightarrow \) DE< EB < CB.
Đáp án : B

Các bài tập cùng chuyên đề
Cho ba điểm \(A,\,B,\,C\) thẳng hàng, \(B\) nằm giữa \(A\) và \(C\). Trên đường thẳng vuông góc với \(AC\) tại \(B\) ta lấy điểm \(H\). Khi đó
Cho \(\Delta ABC\) vuông tại $A,M$ là trung điểm của $AC.$ Gọi $D,E$ lần lượt là hình chiếu của $A$ và $C$ xuống đường thẳng $BM.$ So sánh \(BD + BE\) và $AB.$
Cho \(\Delta ABC\) có $CE$ và $BD$ là hai đường cao. So sánh \(BD + CE\) và \(AB + AC\) ?
Cho \(\Delta ABC\) có \(\widehat C = {90^0}\), \(AC < BC\) , kẻ \(CH \bot AB\). Trên các cạnh $AB$ và $AC$ lấy tương ứng hai điểm $M$ và $N$ sao cho \(BM = BC,CN = CH\). Chọn câu đúng nhất.
Cho góc \(\widehat {xOy} = {60^0},\) \(A\) là điểm trên tia \(Ox,\,B\) là điểm trên tia \(Oy\) \((A,B\) không trùng với \(O).\)
Chọn câu đúng nhất.
Em hãy chọn đáp án sai trong các đáp án sau:












