Nội dung từ Loigiaihay.Com
Cho \(\Delta ABC\) vuông tại $A,M$ là trung điểm của $AC.$ Gọi $D,E$ lần lượt là hình chiếu của $A$ và $C$ xuống đường thẳng $BM.$ So sánh \(BD + BE\) và $AB.$
-
A.
\(BD + BE > 2AB\)
-
B.
\(BD + BE < 2AB\)
-
C.
\(BD + BE = 2AB\)
-
D.
\(BD + BE < AB\)
- Sử dụng quan hệ giữa đường vuông góc với đường xiên
- Sử dụng tính chất của trung điểm
- Chứng minh \(\Delta ADM = \Delta CEM\) (ch - gn)
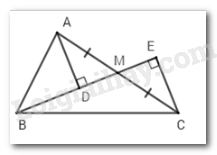
Vì \(\Delta ABM\) vuông tại $A$ (gt) nên \(BA < BM\) (quan hệ giữa đường vuông góc và đường xiên).
Mà \(BM = BD + DM \Rightarrow BA < BD + DM\left( 1 \right)\) .
Mặt khác, \(BM = BE - ME \Rightarrow BA < BE - ME\left( 2 \right)\)
Cộng hai vế của \(\left( 1 \right)\)và \(\left( 2 \right)\) ta được: \(2BA < BD + BE + MD - ME\left( 3 \right)\)
Vì $M$ là trung điểm của $AC$ (gt) \( \Rightarrow AM = MC\) (tính chất trung điểm)
Xét tam giác vuông $ADM$ và tam giác vuông $CEM$ có:
\(AM = MC\left( {cmt} \right)\)
\(\widehat {AMD} = \widehat {EMC}\) (đối đỉnh)
\( \Rightarrow \Delta ADM = \Delta CEM\) (cạnh huyền – góc nhọn)
\( \Rightarrow MD = ME\left( 4 \right)\) (2 cạnh tương ứng)
Từ \(\left( 3 \right)\)và \(\left( 4 \right) \Rightarrow BD + BE > 2AB\)
Đáp án : A

Các bài tập cùng chuyên đề
Cho ba điểm \(A,\,B,\,C\) thẳng hàng, \(B\) nằm giữa \(A\) và \(C\). Trên đường thẳng vuông góc với \(AC\) tại \(B\) ta lấy điểm \(H\). Khi đó
Cho \(\Delta ABC\) có $CE$ và $BD$ là hai đường cao. So sánh \(BD + CE\) và \(AB + AC\) ?
Cho \(\Delta ABC\) vuông tại $A.$ Trên cạnh $AB$ và $AC$ lấy tương ứng hai điểm $D$ và $E$ ($D,E$ không trùng với các đỉnh của \(\Delta ABC\)). Chọn đáp án đúng nhất.
Cho \(\Delta ABC\) có \(\widehat C = {90^0}\), \(AC < BC\) , kẻ \(CH \bot AB\). Trên các cạnh $AB$ và $AC$ lấy tương ứng hai điểm $M$ và $N$ sao cho \(BM = BC,CN = CH\). Chọn câu đúng nhất.
Cho góc \(\widehat {xOy} = {60^0},\) \(A\) là điểm trên tia \(Ox,\,B\) là điểm trên tia \(Oy\) \((A,B\) không trùng với \(O).\)
Chọn câu đúng nhất.
Em hãy chọn đáp án sai trong các đáp án sau:












