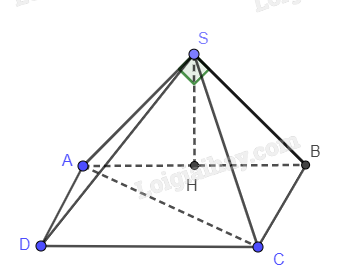
Bài 8.29 trang 83 SGK Toán 11 tập 2 - Cùng khám phá

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình vuông có AC = 2a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm H của cạnh AB và tam giác SAB vuông tại S. Tính thể tích khối chóp này.

Lời giải chi tiết

Ta có:

\(\begin{array}{l}AC = \sqrt {A{B^2} + C{B^2}} \\ \Leftrightarrow 2a = \sqrt {2A{B^2}} \\ \Leftrightarrow 4{a^2} = 2A{B^2}\\ \Leftrightarrow A{B^2} = 2{a^2}\\ \Leftrightarrow AB = \sqrt 2 a\end{array}\)

Xét tam giác SAB vuông tại S:

\(\begin{array}{l}AB = \sqrt {S{A^2} + S{B^2}} \\ \Leftrightarrow \sqrt 2 a = \sqrt {2S{A^2}} \\ \Leftrightarrow 2{a^2} = 2S{A^2}\\ \Leftrightarrow SA = a\end{array}\)

Tam giác vuông SAB có SH là đường cao có:

\(\begin{array}{l}SH.AB = SA.SB\\ \Leftrightarrow SH = \frac{{a.a}}{{\sqrt 2 a}} = \frac{{\sqrt 2 }}{a}a\end{array}\)

\(V = \frac{1}{3}S.h = \frac{1}{3}.A{B^2}.SH = \frac{1}{3}.{\left( {\sqrt 2 a} \right)^2}.\frac{{\sqrt 2 }}{2}a = \frac{{\sqrt 2 }}{3}{a^3}\)