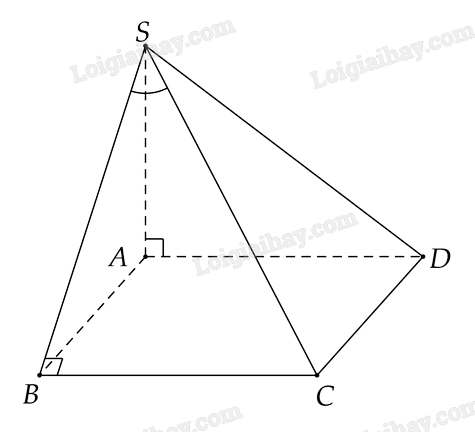
Bài 8.12 trang 63 SGK Toán 11 tập 2 - Cùng khám pháCho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc mặt đáy và \(SA = \sqrt 2 .a\). Đề bài Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc mặt đáy và \(SA = \sqrt 2 .a\).Tính số đo góc giữa SC và (SAB) Phương pháp giải - Xem chi tiết Chứng minh \(BC \bot \left( {SAB} \right)\) từ đó suy ra \(SB\) là hình chiếu của \(SC\) trên \(\left( {SAB} \right)\) Từ đó xác định góc cần tìm là góc \(\widehat {BSC}\) Sử dụng Định lý Pi – ta – go để tính cạnh \(SB\) trong \(\Delta SAB\) vuông tại \(A\) Sử dụng \(\tan \alpha \) để tính góc \(\widehat {BSC}\) trong tam giác \(SBC\) vuông tại \(B\) Lời giải chi tiết
Ta có \(SA \bot BC\) vì \(SA \bot \left( {ABCD} \right)\) Vì \(\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\) Suy ra \(SB\) là hình chiếu vuông góc của \(SC\) trên \(\left( {SAB} \right)\) Vậy góc giữa \(SC\) và \(\left( {SAB} \right)\) là góc giữa \(SC\) và \(SB\) Vậy góc đó là góc \(\widehat {BSC}\) Xét \(\Delta SAB\) vuông tại \(A\) có \(SA = a\sqrt 2 ,AB = a \Rightarrow SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \) Xét \(\Delta SBC\) vuông tại \(B\) có \(\tan \widehat {BSC} = \frac{{BC}}{{SB}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {BSC} = {30^o}\)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
