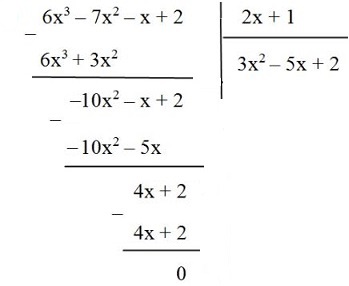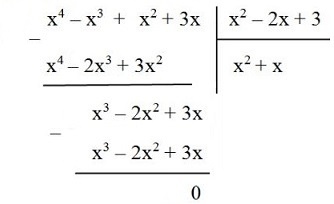Bài 80 trang 33 SGK Toán 8 tập 1

LG a.

\(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\)

Phương pháp giải:

Áp dụng quy tắc chia đa thức một biến đã sắp xếp.

Lời giải chi tiết:

Vậy \((6{x^3}-7{x^2}-x + 2):\left( {2x + 1} \right) = 3{x^2}-5x + 2\)

Cách 2:

Ta có:

\(\begin{array}{l}
6{x^3} - 7{x^2} - x + 2\\
= 6{x^3} + 3{x^2} - 10{x^2} - 5x + 4x + 2\\
= 3{x^2}\left( {2x + 1} \right) - 5x\left( {2x + 1} \right) + 2\left( {2x + 1} \right)\\
= \left( {2x + 1} \right)\left( {3{x^2} - 5x + 2} \right)
\end{array}\)

Khi đó:

\(\begin{array}{l}
\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\\
= \left( {2x + 1} \right)\left( {3{x^2} - 5x + 2} \right):\left( {2x + 1} \right)\\
= 3{x^2} - 5x + 2
\end{array}\)

LG b.

\(\left( {{x^4} - {x^3} + {x^2} + 3x} \right):\left( {{x^2} - 2x + 3} \right)\) ;

Phương pháp giải:

Áp dụng quy tắc chia đa thức một biến đã sắp xếp.

Lời giải chi tiết:

Vậy \(({x^4}\;-{\rm{ }}{x^3}\; + {\rm{ }}{x^2}\; + {\rm{ }}3x){\rm{ }}:{\rm{ }}({x^2}\;-{\rm{ }}2x{\rm{ }} + {\rm{ }}3){\rm{ }} = {\rm{ }}{x^2}\; + {\rm{ }}x\)

Cách 2:

Phân tích \(x^4 – x^3 + x^2 + 3x\) thành nhân tử có chứa \(x^2 + x\)

Ta có:

\(\begin{array}{l}
{x^4} - {x^3} + {x^2} + 3x\\
= {x^4} + {x^3} - 2{x^3} - 2{x^2} + 3{x^2} + 3x\\
= {x^2}\left( {{x^2} + x} \right) - 2x\left( {{x^2} + x} \right) + 3\left( {{x^2} + x} \right)\\
= \left( {{x^2} + x} \right)\left( {{x^2} - 2x + 3} \right)
\end{array}\)

Nên:

\(\begin{array}{l}
\left( {{x^4} - {x^3} + {x^2} + 3x} \right):\left( {{x^2} + x} \right)\\
= \left( {{x^2} + x} \right)\left( {{x^2} - 2x + 3} \right):\left( {{x^2} + x} \right)\\
= {x^2} - 2x + 3
\end{array}\)

LG c.

\(\left( {{x^2} - {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\) .

Phương pháp giải:

Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm và hằng đẳng thức.

Lời giải chi tiết:

\(\left( {{x^2} - {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\)

=\(\left( {{x^2} + 6x + 9 - {y^2}} \right):\left( {x + y + 3} \right)\)

=\(\left[ {\left( {{x^2} + 2x.3 + {3^2}} \right) - {y^2}} \right]:\left( {x + y + 3} \right)\)

=\(\left[ {{{\left( {x + 3} \right)}^2} - {y^2}} \right]:\left( {x + y + 3} \right)\)

=\(\left( {x + 3 - y} \right)\left( {x + 3 + y} \right):\left( {x + y + 3} \right)\)

= \(x + 3 - y\)

= \(x - y + 3\)

HocTot.Nam.Name.Vn