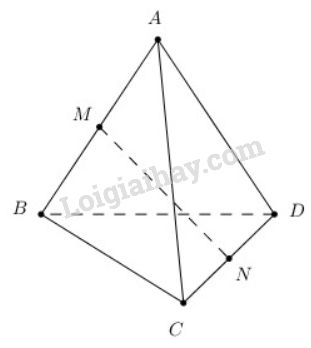
Bài 8 trang 98 SGK Hình học 11Cho tứ diện ABCD có AB = AC = AD ... Đề bài Cho tứ diện ABCDABCD có AB=AC=ADAB=AC=AD và ^BAC=^BAD=600.ˆBAC=ˆBAD=600. Chứng minh rằng: a) AB⊥CDAB⊥CD; b) Nếu M,NM,N lần lượt là trung điểm của ABAB và CDCD thì MN⊥ABMN⊥AB và MN⊥CDMN⊥CD. Video hướng dẫn giải Lời giải chi tiết
a) →AB.→CD=→AB(→AD−→AC)−−→AB.−−→CD=−−→AB(−−→AD−−−→AC) =→AB.→AD−→AB.→AC=−−→AB.−−→AD−−−→AB.−−→AC =AB.AD.cos^BAD−AB.AC.cos^BAC=0=AB.AD.cosˆBAD−AB.AC.cosˆBAC=0 ⇒AB⊥CD⇒AB⊥CD. b) →MN=→MA+→AD+→DN,−−−→MN=−−→MA+−−→AD+−−→DN, (1) →MN=→MB+→BC+→CN.−−−→MN=−−→MB+−−→BC+−−→CN. (2) Cộng (1) với (2) theo vế với vế ta được: 2→MN=(→MA+→MB)+(→AD+→BC)+(→DN+→CN)=→0+(→AD+→BC)+→0=→AD+→BC⇒→MN=12(→AD+→BC)=12(→AD+→AC−→AB) Ta có →AB.→MN=12→AB.(→AD+→AC−→AB) =12(→AB.→AD+→AB.→AC−AB2) =12(AB.AD.cos^BAD+AB.AC.cos^BAC−AB2) =12(AB.AD.cos600+AB.AC.cos600−AB2) =12(12AB2+12AB2−AB2)=0 ⇒AB⊥MN. →MN.→CD=12(→AD+→AC−→AB).(→AD−→AC)=12(→AD2+→AC.→AD−→AB.→AD−→AC.→AD−→AC2+→AB.→AC)=12(AD2−→AB.→AD−AC2+→AB.→AC)=12(AD2−AB.ACcos^BAD−AC2+AB.AC.cos^BAC)=12(AB2−AB2cos600−AB2+AB2cos600)=12.0=0⇒MN⊥CD HocTot.Nam.Name.Vn
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|