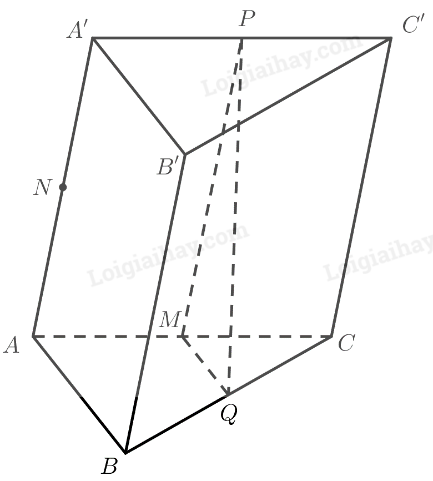
Bài 8 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạoCho hình lăng trụ (ABC.A'B'C'). Gọi (M,N,P,Q) lần lượt là trung điểm của các cạnh (AC,AA',A'C',BC). Ta có: Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M,N,P,Q\) lần lượt là trung điểm của các cạnh \(AC,AA',A'C',BC\). Ta có: A. \(\left( {MNP} \right)\parallel \left( {BCA} \right)\). B. \(\left( {MNQ} \right)\parallel \left( {A'B'C'} \right)\). C. \(\left( {NQP} \right)\parallel \left( {CAB} \right)\). D. \(\left( {MPQ} \right)\parallel \left( {ABA'} \right)\). Phương pháp giải - Xem chi tiết Sử dụng định lí: Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\). Lời giải chi tiết
Ta có: \(M\) là trung điểm của \(AC\) \(Q\) là trung điểm của \(BC\) \( \Rightarrow MQ\) là đường trung bình của tam giác \(ABC\) \(\left. \begin{array}{l} \Rightarrow MQ\parallel AB\\AB \subset \left( {ABA'} \right)\end{array} \right\} \Rightarrow MQ\parallel \left( {ABA'} \right)\) \(M\) là trung điểm của \(AC\) \(P\) là trung điểm của \(A'C'\) \( \Rightarrow MP\) là đường trung bình của hình bình hành \(ACC'A'\) \(\left. \begin{array}{l} \Rightarrow MP\parallel AA'\\AA' \subset \left( {ABA'} \right)\end{array} \right\} \Rightarrow MP\parallel \left( {ABA'} \right)\) \(\left. \begin{array}{l}MQ\parallel \left( {ABA'} \right)\\MP\parallel \left( {ABA'} \right)\\MP,MQ \subset \left( {MPQ} \right)\end{array} \right\} \Rightarrow \left( {MPQ} \right)\parallel \left( {ABA'} \right)\) Chọn D.  Chia sẻ Bình luận
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
|
