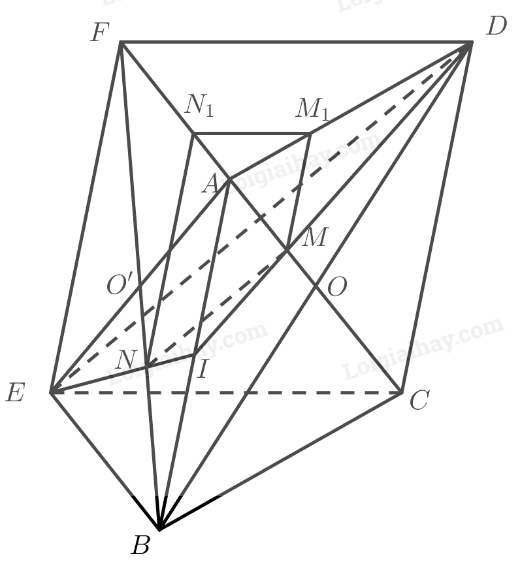
Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo

Đề bài

Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng khác nhau. Lấy các điểm \(M,N\) lần lượt thuộc các đường chéo \(AC\) và \(BF\) sao cho \(MC = 2MA;NF = 2NB\). Qua \(M,N\) kẻ các đường thẳng song song với \(AB\), cắt các cạnh \(AD,AF\) lần lượt tại \({M_1},{N_1}\). Chứng minh rằng:

a) \(MN\parallel DE\);

b) \({M_1}{N_1}\parallel \left( {DEF} \right)\);

c) \(\left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\).

Lời giải chi tiết

a) Vì AI // CD nên \(\frac{{AI}}{{CD}} = \frac{{IM}}{{MD}} = \frac{{AM}}{{MC}} = \frac{1}{2}\) (định lý Thales).

Vì IB // EF nên \(\frac{{IB}}{{EF}} = \frac{{IN}}{{NE}} = \frac{{BN}}{{NF}} = \frac{1}{2}\) (định lý Thales).

Do đó \(\frac{{IM}}{{MD}} = \frac{{IN}}{{NE}} = \frac{1}{2}\), suy ra MN // DE (định lý Thales đảo).

b) Theo giả thiết, AB // \(M{M_1}\) và \(M{M_1}\) không thuộc (ABEF) nên \(M{M_1}\) // (ABEF).

c) Ta có \(M{M_1}\) // AB // EF, suy ra \(M{M_1}\) // (DEF) (1)

Vì \(N{N_1}\) // AB nên \(\frac{{A{N_1}}}{{{N_1}F}} = \frac{{BN}}{{NF}} = \frac{1}{2}\) (định lý Thales).

Vì \(M{M_1}\) // AB nên \(\frac{{A{M_1}}}{{{M_1}D}} = \frac{{AM}}{{MC}} = \frac{1}{2}\) (định lý Thales).

Do đó \(\frac{{A{N_1}}}{{{N_1}F}} = \frac{{A{M_1}}}{{{M_1}D}} = \frac{1}{2}\), suy ra \({M_1}{N_1}\) // DF và \({M_1}{N_1}\) // (DEF) (2).

Mà \(M{M_1}\) cắt \({M_1}{N_1}\) (3).

Từ (1), (2), (3) suy ra \((MN{N_1}{M_1})\) // (DEF).