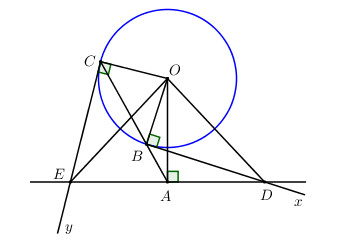
Bài 7 trang 102 Tài liệu dạy – học Toán 9 tập 2Giải bài tập Cho đường tròn (O) và đường thẳng (d) ở ngoài đường tròn. Gọi A là hình chiếu của O trên d. Đề bài Cho đường tròn (O) và đường thẳng (d) ở ngoài đường tròn. Gọi A là hình chiếu của O trên d. Từ A kẻ cát tuyến ABC với đường tròn (B nằm giữa A và C). Hai tiếp tuyến Bx và Cy cắt d lần lượt tại D và E. Chứng minh AE = AD. Phương pháp giải - Xem chi tiết +) Chứng minh tứ giác OAEC và OBAD là tứ giác nội tiếp. +) Chứng minh ^OEC=^ODB. +) Chứng minh ΔvOCE=ΔvOBD⇒OE=OD. +) Sử dụng tính chất: Trong tam giác cân, đường cao đồng thời là trung tuyến. Lời giải chi tiết Xét tứ giác OAEC có: ^OAE+^OCE=900+900=1800⇒Tứ giác OAEC là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bằng 1800) ⇒^OEC=^OAC (1) (hai góc nội tiếp cùng chắn cung OC) Xét tứ giác OBAD có: ^OBD=^OAD=900⇒ Hai điểm A, B cùng nhìn OD dưới góc 900⇒A;B thuộc đường tròn đường kính OD ⇒ Tứ giác OBAD là tứ giác nội tiếp đường tròn đường kính OD ⇒^OAB=^ODB=^OAC (2) Từ (1) và (2) ⇒^OEC=^ODB. Xét ΔOCE và ΔOBD có OC=OB=R;^OCE=^ODB(cmt) ⇒ΔOCE=ΔOBD (cạnh góc vuông – góc nhọn) ⇒OE=OD (2 cạnh tương ứng) ⇒ΔOED cân tại O ⇒ Đường cao OA đồng thời là đường trung tuyến AE=AD (đpcm). HocTot.Nam.Name.Vn
|