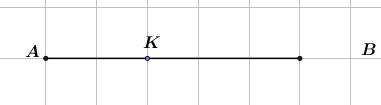
Bài 6 trang 17 SGK Hình học 10Cho hai điểm phân biệt A và B. Tìm điểm K sao cho Đề bài Cho hai điểm phân biệt A và B. Tìm điểm K sao cho:3−−→KA+2−−→KB=→0. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Từ đẳng thức đã cho ta biến đổi tương đương đưa về dạng −−→AK=k−−→AB Sau đó kết luận vị trí điểm K, trong đó +) Nếu k>0 thì −−→AK và −−→AB cùng hướng. +) Nếu k<0 thì −→Ak và −−→AB ngược hướng. Lời giải chi tiết Ta có: 3−−→KA+2−−→KB=→0 ⇒3−−→KA+2(−−→KA+−−→AB)=→0 ⇒5−−→KA+2−−→AB=→0 ⇔−5−−→AK+2−−→AB=→0 ⇔5−−→AK=2−−→AB ⇔−−→AK=25−−→AB Suy ra −−→AK,−−→AB cùng hướng và AK=25AB. Vậy K nằm giữa A và B sao cho AK=25AB.
HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|
