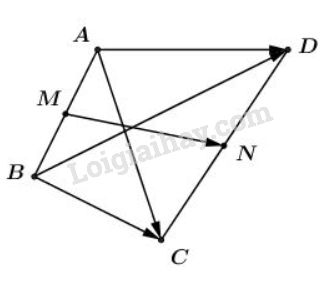
Bài 5 trang 17 SGK Hình học 10

Đề bài

Gọi \(M\) và \(N\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\) của tứ giác \(ABCD\). Chứng minh rằng:

\(2\overrightarrow {MN}  = \overrightarrow {AC}  + \overrightarrow {BD}  = \overrightarrow {BC}  + \overrightarrow {AD} \)

Lời giải chi tiết

   

\(N\) là trung điểm của \(CD\) nên ta có:

\(  \overrightarrow {MC}  + \overrightarrow {MD}=2\overrightarrow {MN}  \)

hay \(2\overrightarrow {MN}=  \overrightarrow {MC}  + \overrightarrow {MD}\)    (1)

Theo quy tắc 3 điểm, ta có:

\(\overrightarrow {MC}  = \overrightarrow {MA}  + \overrightarrow {AC} \)            (2)

\(\overrightarrow {MD}  = \overrightarrow {MB}  + \overrightarrow {BD} \)          (3)

Từ (1), (2), (3) ta có:

\(2\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AC}  + \overrightarrow {MB}  + \overrightarrow {BD}  \)

\(= \left( {\overrightarrow {MA}  + \overrightarrow {MB} } \right) + \overrightarrow {AC}  + \overrightarrow {BD} \) \( = \overrightarrow 0  + \left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right)\) \( = \overrightarrow {AC}  + \overrightarrow {BD} \)

(Do M là trung điểm AB nên \({\overrightarrow {MA}  + \overrightarrow {MB} }=\overrightarrow {0}\))

Chứng minh tương tự, ta có:

\(\begin{array}{l}
2\overrightarrow {MN} = \overrightarrow {MC} + \overrightarrow {MD} \\
= \left( {\overrightarrow {MB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {MA} + \overrightarrow {AD} } \right)\\
= \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {MA} + \overrightarrow {AD} \\
= \left( {\overrightarrow {MB} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {AD} } \right)\\
= \overrightarrow {BC} + \overrightarrow {AD}
\end{array}\)

HocTot.Nam.Name.Vn