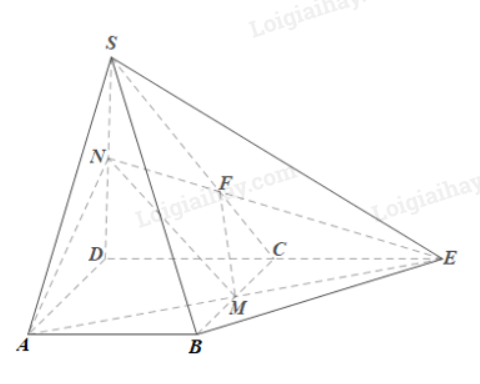
Bài 6 trang 120 SGK Toán 11 tập 1 - Cánh Diều

Đề bài

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, SD. Xác định giao tuyến của mặt phẳng (AMN) với mỗi mặt phẳng sau:

a) (SCD);

b) (SBC).

Lời giải chi tiết

a) Trong mp(ABCD), kéo dài AM cắt DC tại E. Nối SE, BE.

Ta có: E ∈ AM mà AM ⊂ (AMN) nên E ∈ (AMN);

            E ∈ DC mà DC ⊂ (SCD) nên E ∈ (SCD).

Do đó E là giao điểm của hai mặt phẳng (AMN) và (SCD).

Lại có: N ∈ SD và SD ⊂ (SCD) nên N ∈ (SCD).

Mà N ∈ (AMN), nên N cũng là giao điểm của hai mặt phẳng (AMN) và (SCD).

Vậy (AMN) ∩ (SCD) = NE.

b) Trong mp(SCD), gọi F là giao điểm của SC và NE.

Ta có: F ∈ NE mà NE ⊂ (AMN) nên F ∈ (AMN);

           F ∈ SC mà SC ⊂ (SBC) nên F ∈ (SBC).

Do đó F là giao điểm của (AMN) và (SBC).

Lại có: M ∈ BC và BC ⊂ (SBC) nên M ∈ (SBC).

Mà M ∈ (AMN), nên M cũng là giao điểm của hai mặt phẳng (AMN) và (SBC).

Vậy (AMN) ∩ (SBC) = MF.