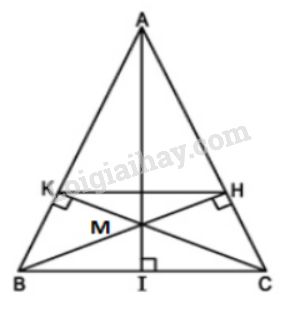
Bài 58 trang 92 SGK Toán 8 tập 2Cho tam giác cân ABC (AB = AC), vẽ các đường cao BH, CK (H.66 Video hướng dẫn giải Cho tam giác cân \(ABC (AB = AC)\), vẽ các đường cao \(BH, CK\) (H.66).
LG a. Chứng minh \(BK = CH\). Phương pháp giải: Áp dụng: Tính chất tam giác cân, định lí TaLet đảo, tính chất trực tâm, tính chất hai tam giác đồng dạng. Lời giải chi tiết: Xét hai tam giác vuông \(BKC\) và \(CHB\) có: \(\widehat {KBC} = \widehat {HCB}\) (\(∆ABC\) cân tại \(A\)) \(BC\) là cạnh chung \( \Rightarrow ∆BKC = ∆CHB\) (cạnh huyền - góc nhọn) \( \Rightarrow BK = CH\) (2 cạnh tương ứng) LG b. Chứng minh \(KH//BC\). Phương pháp giải: Áp dụng: Tính chất tam giác cân, định lí TaLet đảo, tính chất trực tâm, tính chất hai tam giác đồng dạng. Lời giải chi tiết: Ta có : \(AK = AB - BK, AH = AC - HC\) (gt) Mà \(AB = AC\) (\(∆ABC\) cân tại \(A\)) \(BK = CH\) (chứng minh trên) \( \Rightarrow AK = AH\) Do đó : \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}\) \( \Rightarrow KH // BC\) (định lí Ta lét đảo) LG c. Cho biết \(BC = a, AB = AC = b\). Tính độ dài đoạn thẳng \(HK\). Hướng dẫn câu c): - Vẽ thêm đường cao \(AI\), xét hai tam giác đồng dạng \(IAC\) và \(HBC\) rồi tính \(CH\). - Tiếp theo, xét hai tam giác đồng dạng \(AKH\) và \(ABC\) rồi tính \(HK\). Phương pháp giải: Áp dụng: Tính chất tam giác cân, định lí TaLet đảo, tính chất trực tâm, tính chất hai tam giác đồng dạng. Lời giải chi tiết: \(BH\) cắt \(CK\) tại \(M\) \( \Rightarrow M\) là trực tâm của \(∆ABC\) (định nghĩa trực tâm) \( \Rightarrow AM ⊥ BC\) tại \(I\) (tính chất trực tâm) Ta có : \(∆AIC ∽ ∆BHC \,(g-g)\) vì \(\left\{ {\matrix{{\widehat I = \widehat H = {{90}^0}} \cr {\widehat C\;chung} \cr} } \right.\) \( \Rightarrow \dfrac{{IC}}{{HC}} = \dfrac{{AC}}{{BC}}\) (tính chất hai tam giác đồng dạng)
HocTot.Nam.Name.Vn
|