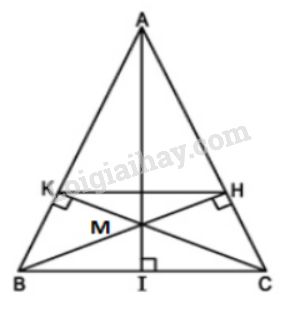
Bài 58 trang 92 SGK Toán 8 tập 2

LG a.

Chứng minh $BK = CH$.

Phương pháp giải:

Áp dụng: Tính chất tam giác cân,  định lí TaLet đảo, tính chất trực tâm, tính chất hai tam giác đồng dạng.

Lời giải chi tiết:

Xét hai tam giác vuông $BKC$ và $CHB$ có:

$\widehat {KBC} = \widehat {HCB}$ ($∆ABC$ cân tại $A$)

$BC$ là cạnh chung 

$\Rightarrow ∆BKC = ∆CHB$ (cạnh huyền - góc nhọn)

$\Rightarrow BK = CH$ (2 cạnh tương ứng)

LG b.

Chứng minh $KH//BC$.

Phương pháp giải:

Áp dụng: Tính chất tam giác cân,  định lí TaLet đảo, tính chất trực tâm, tính chất hai tam giác đồng dạng.

Lời giải chi tiết:

Ta có : $AK = AB - BK, AH = AC - HC$ (gt)

Mà $AB = AC$ ($∆ABC$ cân tại $A$)

      $BK = CH$ (chứng minh trên) 

$\Rightarrow  AK = AH$

Do đó : $\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}$ $\Rightarrow KH // BC$ (định lí Ta lét đảo)

LG c.

Cho biết $BC = a, AB = AC = b$. Tính độ dài đoạn thẳng $HK$.

Hướng dẫn câu c):

- Vẽ thêm đường cao $AI$, xét hai tam giác đồng dạng $IAC$ và $HBC$ rồi tính $CH$.

- Tiếp theo, xét hai tam giác đồng dạng $AKH$ và $ABC$ rồi tính $HK$.

Phương pháp giải:

Áp dụng: Tính chất tam giác cân,  định lí TaLet đảo, tính chất trực tâm, tính chất hai tam giác đồng dạng.

Lời giải chi tiết:

 $BH$ cắt $CK$ tại $M$

$\Rightarrow M$ là trực tâm của $∆ABC$ (định nghĩa trực tâm)

$\Rightarrow AM ⊥ BC$ tại $I$ (tính chất trực tâm)

Ta có : $∆AIC ∽ ∆BHC \,(g-g)$ vì $\left\{ {\matrix{{\widehat I = \widehat H = {{90}^0}} \cr {\widehat C\;chung} \cr} } \right.$

$\Rightarrow \dfrac{{IC}}{{HC}} = \dfrac{{AC}}{{BC}}$ (tính chất hai tam giác đồng dạng)

HocTot.Nam.Name.Vn