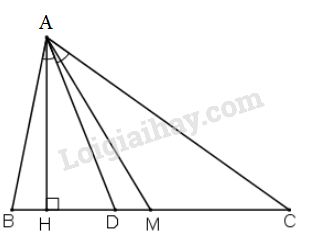
Bài 57 trang 92 SGK Toán 8 tập 2

Đề bài

Cho tam giác $ABC (AB < AC)$. Vẽ đường cao $AH$, đường phân giác $AD$, đường trung tuyến $AM$. Có nhận xét gì về vị trí của ba điểm $H, D, M$.

Lời giải chi tiết

+ Nhận xét: $D$ luôn nằm giữa $H$ và $M$.

+ Chứng minh:

$AD$ là đường phân giác của $∆ABC$.

$\Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{DB}}{{DC}}$ (tính chất đường phân giác của tam giác)

Mà $AB < AC$ (giả thiết)

$\Rightarrow DB < DC$ $\Rightarrow  DB + DC < DC + DC$

$\Rightarrow BD + DC < 2DC$ hay $BC < 2DC$ 

$\Rightarrow  DC >\dfrac{{BC}}{2}$

Mà $MC = \dfrac{{BC}}{2}$ ($M$ là trung điểm của $BC$)

$\Rightarrow DC > MC$ $\Rightarrow M$ nằm giữa $D$ và $C$ (1)

+ Mặt khác: $\widehat {CAH} = {90^0} - \hat C$ ($∆CAH$ vuông tại $H$)

$\hat A + \hat B + \hat C = {180^0}$ (tổng 3 góc ∆ABC)

$\Rightarrow \widehat {CAH} = \dfrac{{\widehat A + \widehat B + \widehat C}}{2} - \widehat C$

$\Rightarrow \widehat {CAH} = \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B}}{2} - \dfrac{{\widehat C}}{2}$$\, = \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B - \widehat C}}{2}$

Vì $AB < AC$ $\Rightarrow \widehat C < \widehat B$ ( quan hệ giữa cạnh và góc đối diện trong tam giác)

$\Rightarrow \frac{\widehat B - \widehat C}{2} > 0$

Do đó: $\widehat {CAH} >  \dfrac{{\widehat A}}{2}$ hay $\widehat {CAH} > \widehat {CAD}$

$\Rightarrow$ Tia $AD$ nằm giữa hai tia $AH$ và $AC$

Do đó $D$ nằm giữa hai điểm $H$ và $C$ (2)

Từ (1) và (2) suy ra $D$ nằm giữa $H$ và $M.$

HocTot.Nam.Name.Vn