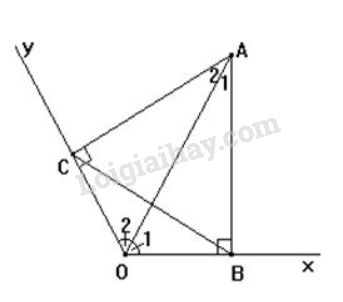
Bài 52 trang 128 SGK Toán 7 tập 1Cho góc xOy có số đo, điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox(B thuộc Ox), kẻ AC vuông góc với Oy(C thuộc Oy). GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Cho góc xOyxOy có số đo 12001200, điểm AA thuộc tia phân giác của góc đó. Kẻ ABAB vuông góc với OxOx (BB thuộc OxOx), kẻ ACAC vuông góc với OyOy (CC thuộc OyOy). Tam giác ABCABC là tam giác gì ? Vì sao? Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: - Nếu cạnh huyền và góc nhọn của tam giác vuông này bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. - Tam giác cân có một góc bằng 60o60o thì tam giác đó là tam giác đều. - Định lí tổng ba góc của một tam giác bằng 180o180o. Lời giải chi tiết
Tam giác ACOACO vuông tại CC. Tam giác ABOABO vuông tại BB Xét hai tam giác vuông ACOACO và ABOABO có: +) ^O1=^O2ˆO1=ˆO2 (Vì OAOA là tia phân giác góc xOyxOy) +) AOAO chung ⇒∆ACO=∆ABO⇒ΔACO=ΔABO (cạnh huyền-góc nhọn) ⇒AC=AB⇒AC=AB (hai cạnh tương ứng); ^A1=^A2ˆA1=ˆA2 (hai góc tương ứng) Ta có ^O1=12^xOy=12.1200=600ˆO1=12ˆxOy=12.1200=600 (vì OAOA là tia phân giác góc xOyxOy) Áp dụng định lí tổng ba góc của một tam giác vào ΔOBAΔOBA ta có: ^O1+ˆB+^A1=1800⇒^A1=1800−^O1−ˆB=1800−600−900=300 Do đó: ^A1=^A2=300 Hay ^BAC=^A1+^A2=300+300=600 Vì ∆ABC có AC=AB nên ∆ABC cân tại A. Mà ^BAC=600 nên ∆ABC là tam giác đều.
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|