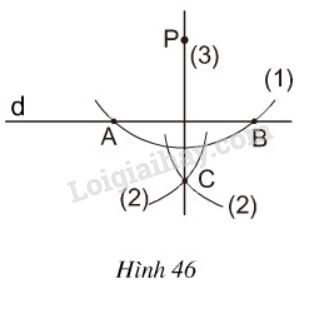
Bài 51 trang 77 SGK Toán 7 tập 2Cho đường thẳng d và điểm P không nằm trên d Đề bài Cho đường thẳng dd và điểm PP không nằm trên dd. Hình 46 minh họa cho cách dựng: đường thẳng đi qua điểm PP và vuông góc với đường thẳng dd bằng thước và compa như sau: (1) Vẽ đường tròn tâm PP với bán kính thích hợp sao cho nó có cắt dd tại hai điểm AA và BB (2) Vẽ hai đường tròn với bán kính bằng nhau có tâm AA và BB sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C(C≠P)C(C≠P). (3) Vẽ đường thẳng PCPC Em hãy chứng minh đường thẳng PCPC vuông góc với dd. Đố: Tìm thêm một cách dựng nữa (bằng thước và compa)
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng định lí 2: Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. Lời giải chi tiết a)
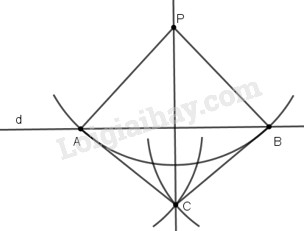
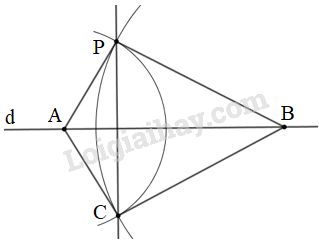
A,BA,B nằm trên cung tròn có tâm PP nên PA=PB.PA=PB. Do đó P nằm trên đường trung trực của AB (Theo định lí 22) CC là giao điểm của 22 cung có bán kính bằng nhau có tâm tại AA và tại BB nên CA=CB.CA=CB. Do đó C nằm trên đường trung trực của AB (Theo định lí 22) ⇒⇒ P;CP;C đều nằm trên đường trung trực của AB. ⇒⇒ Đường thẳng CPCP là đường trung trực của ABAB Do đó: PC⊥dPC⊥d b) Một cách vẽ khác - Lấy hai điểm A,BA,B bất kì trên d.d. - Vẽ cung tròn tâm AA bán kính APAP, cung tròn tâm BB bán kính BPBP. Hai cung tròn cắt nhau tại CC (CC khác PP). - Vẽ đường thẳng PCPC. Khi đó PCPC là đường đi qua PP và vuông góc với d.d.
Chứng minh : PA=CAPA=CA (vì P,CP,C cùng thuộc cung tròn tâm AA bán kính PAPA) ⇒A⇒A thuộc đường trung trực của PCPC (Theo định lí 2) PB=CBPB=CB (vì P,CP,C cùng thuộc cung tròn tâm BB bán kính PBPB) ⇒B⇒B thuộc đường trung trực của PCPC (Theo định lí 2) ⇒AB⇒AB là đường trung trực của PCPC ⇒PC⏊AB hay PC⏊d. HocTot.Nam.Name.Vn
|