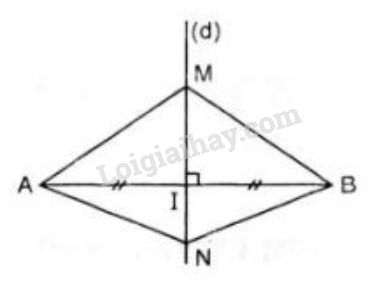
Bài 47 trang 76 SGK Toán 7 tập 2Cho hai điểm M, N nằm trên đường trung trực Đề bài Cho hai điểm M,N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ∆AMN=∆BMN. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng định lí 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó. Lời giải chi tiết
Vì M thuộc đường trung trực của AB nên MA=MB (Theo định lí 1) N thuộc đường trung trực của AB nên NA=NB (Theo định lí 1) Xét ∆AMN và ∆BMN ta có: +) MA=MB (chứng minh trên) +) NA=NB (chứng minh trên) +) MN chung Vậy ∆AMN=∆BMN (c.c.c) (điều phải chứng minh). HocTot.Nam.Name.Vn
|