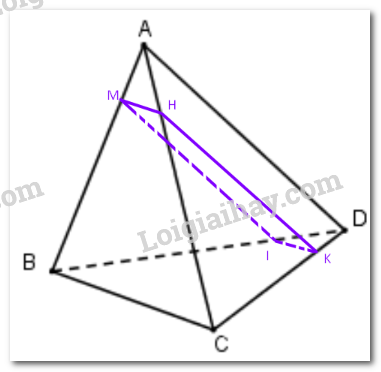
Bài 4.46 trang 103 SGK Toán 11 tập 1 - Kết nối tri thứcCho tứ diện ABCD. Trên cạnh AB lấy điểm M sao cho BM = 3AM. Mặt phẳng (P) đi qua M song song với hai đường thẳng AD và BC. a) Xác định giao điểm K của mặt phẳng (P) với đường thẳng CD. b) Tính tỉ số (frac{{KC}}{{CD}}). Đề bài Cho tứ diện ABCD. Trên cạnh AB lấy điểm M sao cho BM = 3AM. Mặt phẳng (P) đi qua M song song với hai đường thẳng AD và BC. a) Xác định giao điểm K của mặt phẳng (P) với đường thẳng CD. b) Tính tỉ số \(\frac{{KC}}{{CD}}\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P). Lời giải chi tiết
a) Qua M kẻ MH// BC, MI // AD. mp(P) đi qua M song song với hai đường thẳng AD và BC. Suy ra mp(P) chứa MH và MI. Ta có: \(\begin{array}{l}\left( {ABC} \right) \cap (P) = MH\\\left( {ABC} \right) \cap (BCD) = BC\end{array}\) \( \Rightarrow \)MH//BC. Suy ra, giao tuyến của (P) và (BCD) song song với BC và MH. Qua I kẻ IK // BC (K thuộc CD) Vậy giao điểm của (P) và CD là K. b) Ta có: \(\begin{array}{l}\left( {ABD} \right) \cap (P) = MI\\\left( {ABD} \right) \cap (ACD) = AD\\(P) \cap (ACD) = HK\end{array}\) \( \Rightarrow \)MI//AD, HK //MI Tứ giác MHKI có: MH // KI, MI // HK Suy ra MHKI là hình bình hành \( \Rightarrow \) MH = KI. Xét tam giác ABC có MH // BC, BM = 3AM Suy ra BC = 4MH suy ra BC = 4KI. Xét tam giác BCD có IK // BC, BC = 4KI suy ra \(\frac{{KC}}{{CD}} = \frac{3}{4}\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
