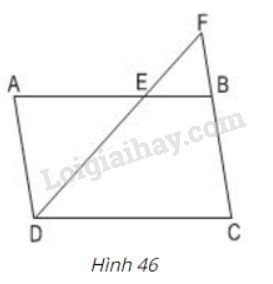
Bài 43 trang 80 SGK Toán 8 tập 2Cho hình bình hành ABCD(h46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Video hướng dẫn giải Cho hình bình hành \(ABCD\) (h46) có độ dài các cạnh \(AB = 12cm, BC = 7cm.\) Trên cạnh \(AB\) lấy một điểm \(E\) sao cho \(AE = 8cm\). Đường thẳng \(DE\) cắt \(CB\) kéo dài tại \(F\),
LG a. Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng. Phương pháp giải: Áp dụng - Định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho. Giải chi tiết: Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho. \(BE // DC\) (vì \(ABCD\) là hình bình hành) \(\Rightarrow ∆BFE ∽ ∆CFD\) (1) \(AD // BF\) (vì \(ABCD\) là hình bình hành) \( \Rightarrow ∆ADE ∽ ∆BFE\) (2) Từ (1) và (2) suy ra \(∆ADE ∽ ∆CFD\) LG b. Tính độ dài đoạn \(EF\) và \(BF\), biết rằng \(DE = 10\,cm\). Phương pháp giải: Áp dụng: Tính chất hai tam giác đồng dạng. Giải chi tiết: Ta có: \(BE = AB - AE = 12 - 8 = 4cm\); \(AD=BC=7cm\) (vì ABCD là hình bình hành) Ta có: \(∆ADE ∽ ∆BFE (cmt)\) \( \Rightarrow \dfrac{AE}{BE} = \dfrac{AD}{BF} = \dfrac{DE}{EF}\) (tính chất tam giác đồng dạng) \(\Rightarrow \dfrac{8}{4} = \dfrac{7}{BF} = \dfrac{10}{EF}\) \(\eqalign{ HocTot.Nam.Name.Vn
|