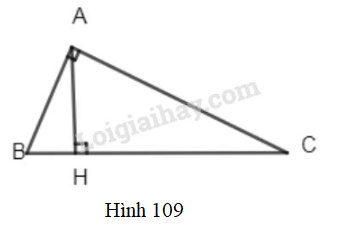
Bài 42 trang 124 SGK Toán 7 tập 1

Đề bài

Cho tam giác $ABC$ có $\widehat{A}= 90^o$ (h.109), kẻ $AH$ vuông góc với $BC$ $(H∈BC).$ Các tam giác $AHC$ và $BAC$ có $AC$ là cạnh chung, $\widehat C$ là góc chung,  $\widehat{AHC}=\widehat{BAC}= 90^o$, nhưng hai tam giác không bằng nhau. Tại sao ở đây không áp dụng trường hợp góc cạnh góc để kết luận $∆AHC= ∆BAC?$ 

Lời giải chi tiết

Xét $∆AHC$ và $∆BAC$ có:

+) $AC$ là cạnh chung 

+) $\widehat{C}$ là góc chung

+) $\widehat{AHC}=\widehat{BAC}=90^o$    

Nhưng hai tam giác không bằng nhau vì $\widehat{AHC}$ không phải là góc kề với cạnh $AC$ nên ta không thể suy ra hai tam giác này bằng nhau theo trường hợp góc - cạnh - góc.

HocTot.Nam.Name.Vn