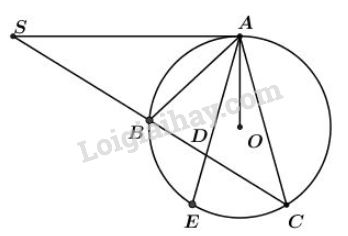
Bài 40 trang 83 SGK Toán 9 tập 2

Đề bài

Qua điểm \(S\) nằm bên ngoài đường tròn \((O)\), vẽ tiếp tuyến \(SA\) và cát tuyến \(SBC\) của đường tròn. Tia phân giác của \(\widehat{BAC}\) cắt dây \(BC\) tại \(D.\) Chứng minh \(SA = SD.\)

Lời giải chi tiết

                 

Gọi \(E\) là giao điểm thứ hai của \(AD\) với đường tròn \((O).\)

Xét đường tròn \((O)\) ta có: 

 +) \(\widehat{ADS}\) là góc có đỉnh nằm trong đường tròn chắn cung \(AB\) và \(CE.\)

\(\Rightarrow \widehat {ADS}=\dfrac{sđ\overparen{AB}+sđ\overparen{CE}}{2}.\)  (1)

+) \(\widehat{SAD}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung \(AE.\)

\(\Rightarrow \widehat {SAD}=\dfrac{1}{2} sđ\overparen{AE}.\)  (2)

+) Có: \(\widehat {BAE} = \widehat {EAC}\) (do \(AE\) là phân giác góc \(BAC\))

\(\Rightarrow \) \(\overparen{BE}=\overparen{EC}\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau).

\(\Rightarrow sđ\overparen{AB} + sđ\overparen{BE}= sđ\overparen{AB} + sđ\overparen{EC}\)\( sđ\overparen{AE}\) (3)

Từ (1) và (3) \(\Rightarrow \widehat {ADS}=\dfrac{sđ\overparen{AE}}{2}\) (4)

Từ (2) và (4) \(\Rightarrow\widehat {ADS}=\widehat {SAD}\)\(\Rightarrow\) tam giác \(SDA\) cân tại \(S\) hay \(SA=SD\).