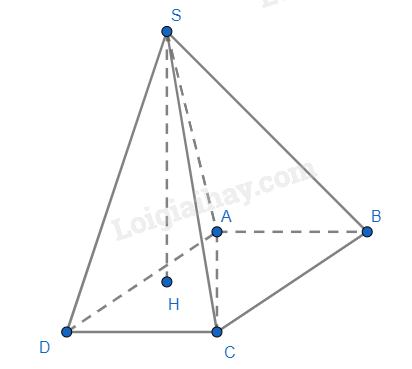
Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh DiềuCho tứ diện ABCD có (AB bot (BCD),BC bot CD). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng: Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho hình chóp S.ABCD có đáy là hình bình hành. Tam giác ABC nhọn có trực tâm H là hình chiếu của S trên (ABCD). Chứng minh rằng: a) SA \(\bot\) AD; b) SC \(\bot\) CD. Phương pháp giải - Xem chi tiết Dựa vào quan hệ từ vuông góc đến song song trong không gian để chứng minh Lời giải chi tiết
a) Vì SH \(\bot\) (ABCD) nên AH là hình chiếu của SA trên mặt phẳng (ABCD). Mà AH \(\bot\) BC, AD // BC => AH \(\bot\) AD. Theo định lí ba đường vuông góc ta có SA \(\bot\) AD. b) Vì SH \(\bot\) (ABCD) nên HC là hình chiếu của SC trên mặt phẳng (ABCD). Mà AB \(\bot\) HC, AB // CD => HC \(\bot\) CD. Theo định lí 3 đường vuông góc ta có SC \(\bot\) CD.  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
|
