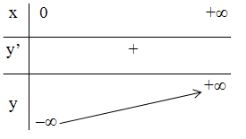
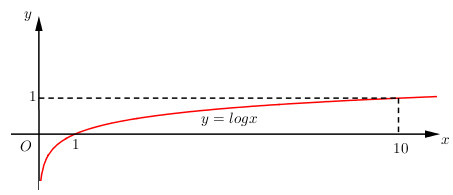
Giải bài 4 trang 78 SGK Giải tích 12

LG a

a) \(y = \log x\);

Phương pháp giải:

Các bước khảo sát và vẽ đồ thị hàm số:

Bước 1: Tập xác định.

Bước 2: Sự biến thiên.

- Tính \(y'\), tìm các điểm mà tại đó \(y'\) bằng 0 hoặc không xác định.

- Xét dấu \(y'\) và suy ra các khoảng đơn điệu của đồ thị hàm số.

- Tính các giới hạn đặc biệt: Giới hạn tại vô cực và giới hạn tại các điểm mà hàm số không xác định.

- Tìm các tiệm cận của đồ thị hàm số (nếu có).

- Lập bảng biến thiên.

Bước 3: Đồ thị.

- Tìm giao điểm của đồ thị hàm số với các trục tọa độ (nếu có).

- Vẽ đồ thị hàm số dựa vào các yếu tố ở trên.

Lời giải chi tiết:

Đồ thị hàm số \(y = \log x\).

*) Tập xác định: \(D=(0;+\infty)\)

*) Sự biến thiên:

\(y' = {1 \over {x\ln 10}} > 0,\forall x \in D\)

- Hàm số đồng biến trên khoảng \((0;+\infty)\)

- Giới hạn đặc biệt:

  \(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} y = - \infty \cr 
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr} \)

Hàm số có tiệm cận đứng là: \(x=0\)

- Bảng biến thiên:

*) Đồ thị:

Đồ thị hàm số nằm hoàn toàn bên phải trục tung) nhận trục tung làm tiệm cận đứng, cắt trục hoành tại điểm \((1;0)\) và đi qua điểm \((10;1)\), \((\dfrac{1}{10}; -1)\).

LG b

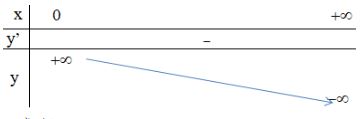
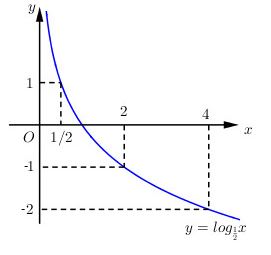
b) y = \(\log_{\frac{1}{2}}x\).

Lời giải chi tiết:

Đồ thị hàm số \(y = \log_{\frac{1}{2}}x\).

*) Tập xác định: \(D=(0;+\infty)\)

*) Sự biến thiên:

\(y' =  \dfrac {-1}  {x\ln 2} < 0,\forall x \in D\)

- Hàm số nghịch biến trên khoảng \((0;+\infty)\)

- Giới hạn: 

  \(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \cr 
& \mathop {\lim }\limits_{x \to + \infty } y = - \infty \cr} \)

Hàm số có tiệm cận đứng \(x=0\).

- Bảng biến thiên:

*) Đồ thị:

Đồ thị hàm số nằm hoàn toàn bên phải trục tung (nhận trục tung làm tiệm cận đứng), cắt trục hoành tại điểm \((1;0)\) và đi qua điểm \((\dfrac{1}{2};1)\), điểm phụ \((2;-1)\), \((4.-2)\), \((\dfrac{1}{4}; 2)\).

HocTot.Nam.Name.Vn