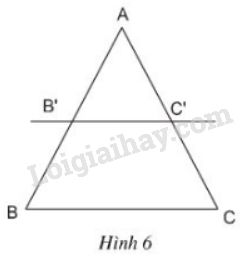
Bài 4 trang 59 SGK Toán 8 tập 2Cho biết AB'/AB= AC'/AC Video hướng dẫn giải Cho biết \(\dfrac{AB'}{AB} = \dfrac{AC'}{AC}\) (h.6)
Chứng minh rằng: LG a. \(\dfrac{AB'}{B'B}= \dfrac{AC'}{C'C}\) Phương pháp giải: - Áp dụng định lí TaLet và tính chất dãy tỉ số bằng nhau. Lời giải chi tiết: Ta có: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\) (giả thiết) \( \Rightarrow \dfrac{AC}{AC'}=\dfrac{AB}{AB'}\) \( \Rightarrow \dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AB}}{{AB'}} - 1\) Ta có: \(\dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AC - AC'}}{{AC'}} = \dfrac{{C'C}}{{AC'}}\) \(\dfrac{{AB}}{{AB'}} - 1 = \dfrac{{AB - AB'}}{{AB'}} = \dfrac{{B'B}}{{AB'}}\) \( \Rightarrow \dfrac{{C'C}}{{AC'}} = \dfrac{{B'B}}{{AB'}} \Rightarrow \dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}\) (điều phải chứng minh). LG b. \(\dfrac{BB'}{AB} = \dfrac{CC'}{AC}\). Phương pháp giải: - Áp dụng định lí TaLet và tính chất dãy tỉ số bằng nhau. Lời giải chi tiết: Vì \(\dfrac{AB'}{AB} = \dfrac{AC'}{AC}\) Mà \(AB' = AB - B'B, AC' = AC - C'C\) \(\dfrac{AB-BB'}{AB} = \dfrac{AC -CC'}{AC}\) \( \Rightarrow 1 - \dfrac{{BB'}}{{AB}} = 1 - \dfrac{{CC'}}{{AC}}\) \( \Rightarrow \dfrac{BB'}{AB}= \dfrac{CC'}{AC}\) (điều phải chứng minh). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
