Bài 4 trang 50 SGK Hình học 12

Đề bài

Hình chóp \(S.ABC\) có một mặt cầu tiếp xúc với các cạnh \(SA, SB, SC\) và tiếp xúc với ba cạnh \(AB, BC, CA\) tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều.

Lời giải chi tiết

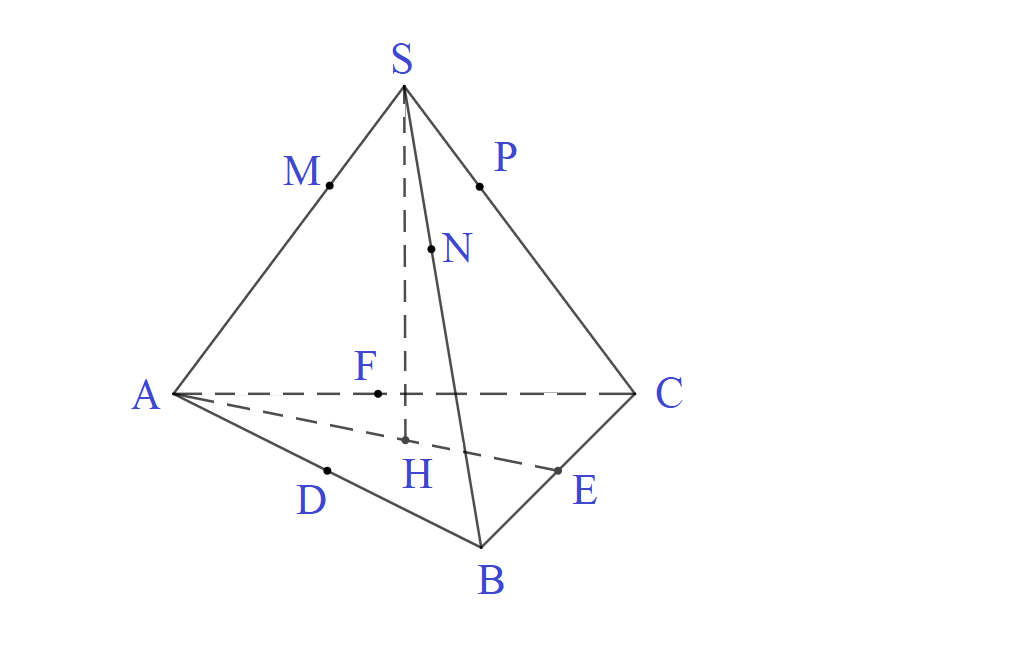
Gọi \(M, N, P\) theo thứ tự là các tiếp điểm của mặt cầu với các cạnh \(SA, SB, SC\); \(D, E, F\) theo thứ tự là trung điểm của các cạnh \(AB, BC, CA\), các điểm \(D, E, F\) đồng thời cũng là tiếp điểm của mặt cầu với các cạnh \(AB, BC, CA\).

Ta có:

\(AD = AF\) (Tính chất hai tiếp tuyến cắt nhau)  \(\Rightarrow AB = AC\)

Tương tự: \(BD = BE \Rightarrow  BC = AB\)

\( \Rightarrow  AB = BC = CA\) hay \(△ABC\) là tam giác đều  (1)

Lại có \(AM = AD; BN = BD = AD\)

và \(SM = SN = SP\)

\( \Rightarrow  SM + AM = SN + NB\) hay \(SA = SB\)

Chứng minh tương tự ta có: \(SA = SB = SC\).     (2)

Từ (1) và (2) suy ra hình chóp \(S.ABC\) là chóp tam giác đều.

HocTot.Nam.Name.Vn