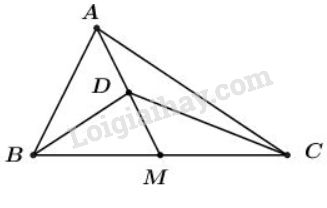
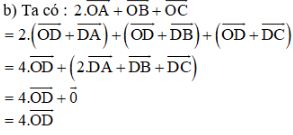Bài 4 trang 17 SGK Hình học 10

LG a

\(2\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = \overrightarrow 0 \)

Phương pháp giải:

Với \(M\) là trung điểm của \(AB\) ta có:

+) \(\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 .\)

+) Với mọi điểm \(O\) bất kì ta có: \(\overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OM} .\)

Lời giải chi tiết:

Vì \(M\) là trung điểm của \(BC\) nên:

Ta có:

\(\overrightarrow {DB}  + \overrightarrow {DC}  = 2\overrightarrow {DM} \)

Mặt khác, do \(D\) là trung điểm của đoạn \(AM\) nên

\(\overrightarrow {DM}  =  - \overrightarrow {DA} \) \(\Leftrightarrow \overrightarrow {DM}  + \overrightarrow {DA}  = \overrightarrow 0 \)

Khi đó: \(2\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = 2\overrightarrow {DA}  + 2\overrightarrow {DM}  \)\(= 2\left( {\overrightarrow {DA}  + \overrightarrow {DM} } \right) = \overrightarrow 0 \)

LG b

\(2\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = 4\overrightarrow {OD} \), với \(O\) là điểm tùy ý.

Phương pháp giải:

Với \(M\) là trung điểm của \(AB\) ta có:

+) \(\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 .\)

+) Với mọi điểm \(O\) bất kì ta có: \(\overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OM} .\)

Lời giải chi tiết:

Ta có:

Cách khác:

\(\eqalign{
& 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \cr} \)

\(\begin{array}{l}
\Leftrightarrow 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} - 4\overrightarrow {OD} = \overrightarrow 0 \\
\Leftrightarrow 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} - 2\overrightarrow {OD} - \overrightarrow {OD} - \overrightarrow {OD} = \overrightarrow 0 \\
\Leftrightarrow \left( {2\overrightarrow {OA} - 2\overrightarrow {OD} } \right) + \left( {\overrightarrow {OB} - \overrightarrow {OD} } \right) + \left( {\overrightarrow {OC} - \overrightarrow {OD} } \right) = \overrightarrow 0 \\
\Leftrightarrow 2\left( {\overrightarrow {OA} - \overrightarrow {OD} } \right) + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \\
\Leftrightarrow 2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0
\end{array}\)

(Đúng theo câu a) 

Vậy: \(2\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = 4\overrightarrow {OD} \), với \(O\) là điểm tùy ý

HocTot.Nam.Name.Vn