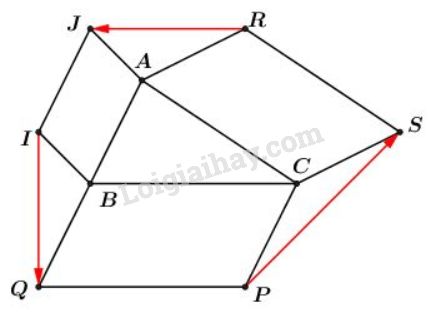
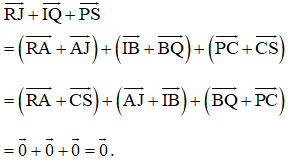Bài 4 trang 12 SGK Hình học 10

Đề bài

Cho tam giác \(ABC\). Bên ngoài tam giác vẽ các hình bình hành \(ABIJ, BCPQ, CARS\). Chứng minh rằng \(\overrightarrow{RJ} + \overrightarrow{IQ} + \overrightarrow{PS}=  \overrightarrow{0}.\)

Lời giải chi tiết

Ta xét tổng:

\((\overrightarrow{RJ}  +\overrightarrow{IQ}  +\overrightarrow{PS})+ ( \overrightarrow{JI}+ \overrightarrow{QP}+\overrightarrow{SR}) \)

\(=\overrightarrow{RJ}  +\overrightarrow{IQ}  +\overrightarrow{PS}+ \overrightarrow{JI}+ \overrightarrow{QP}+\overrightarrow{SR}\)

\(\begin{array}{l}
= \left( {\overrightarrow {RJ} + \overrightarrow {JI} } \right) + \left( {\overrightarrow {IQ} + \overrightarrow {QP} } \right) + \left( {\overrightarrow {PS} + \overrightarrow {SR} } \right)\\
= \overrightarrow {RI} + \overrightarrow {IP} + \overrightarrow {PR} \\
= \overrightarrow {RP} + \overrightarrow {PR}
\end{array}\)

\(= \overrightarrow{RR}= \overrightarrow{0}\)(1)

Mặt khác, ta có \(ABIJ, BCPQ\) và \(CARS\) là các hình bình hành nên:

\(\overrightarrow{JI}  = \overrightarrow{AB}\)

\(\overrightarrow{QP} = \overrightarrow{BC}\)

\(\overrightarrow{SR}= \overrightarrow{CA}\)

\(\Rightarrow \overrightarrow{JI}+\overrightarrow{QP}+\overrightarrow{SR}\)\(= \overrightarrow{AB}+ \overrightarrow{BC}+\overrightarrow{CA}= \overrightarrow{AA}= \overrightarrow{0}\)  (2)

Từ (1) và (2) suy ra : 

\(\overrightarrow{RJ} + \overrightarrow{IQ} + \overrightarrow{PS}\)\(=  \overrightarrow{0}.\) (đpcm)

Cách khác:

Ta có:

AJIB là hình bình hành nên \(\overrightarrow {AJ}  = \overrightarrow {BI} \)

\( \Rightarrow \overrightarrow {AJ}  + \overrightarrow {IB}  = \overrightarrow {BI}  + \overrightarrow {IB}  = \overrightarrow {BB}  = \overrightarrow 0 \)

Tương tự như vậy:

BCPQ là hình bình hành nên \(\overrightarrow {BQ}  + \overrightarrow {PC}  = \overrightarrow 0 \)

CARS là hình bình hành nên \(\overrightarrow {CS}  + \overrightarrow {RA}  = \overrightarrow 0 \)

Do đó:

HocTot.Nam.Name.Vn