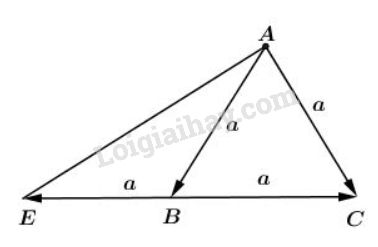
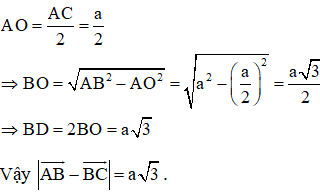Bài 5 trang 12 SGK Hình học 10Cho tam giác ABC cạnh a Đề bài Cho tam giác ABC đều cạnh a. Tính độ dài của các vectơ −−→AB+−−→BC và −−→AB−−−→BC. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Với quy tắc ba điểm tùy ý A,B,C ta luôn có: +)−−→AB+−−→BC=−−→AC (quy tắc ba điểm). +)−−→AB−−−→AC=−−→CB (quy tắc trừ). Lời giải chi tiết
Ta có −−→AB+−−→BC=−−→AC (quy tắc 3 điểm) Suy ra ∣∣∣−−→AB+−−→BC∣∣∣=∣∣∣−−→AC∣∣∣=a. Ta có: −−→AB−−−→BC=−−→AB+−−→CB. Trên tia CB, lấy điểm E sao cho −−→BE=−−→CB. ⇒−−→AB−−−→BC=−−→AB+−−→CB =−−→AB+−−→BE=−−→AE Xét tam giác EAC ta có: đường trung tuyến AB bằng nửa cạnh CE nên là tam giác vuông tại A Áp dụng định lý Pitago ta có: AE2+AC2=CE2 ⇔AE=√CE2−AC2 Mà AC=a,CE=2a, Suy ra AE=√4a2−a2=a√3. Vậy ∣∣∣−−→AB−−−→BC∣∣∣=∣∣∣−−→AE∣∣∣=a√3. Cách khác:
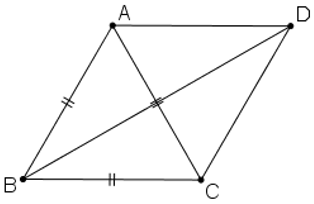
Dựng hình bình hành ABCD ta có: −−→AB−−−→BC=−−→AB+−−→CB=−−→AB+−−→DA=−−→DA+−−→AB=−−→DB⇒∣∣∣−−→AB−−−→BC∣∣∣=∣∣∣−−→DB∣∣∣=DB + Tính BD: Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi. ⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|
