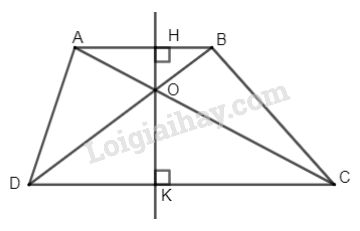
Bài 39 trang 79 SGK Toán 8 tập 2

Đề bài

Cho hình thang $ABCD (AB//CD)$. Gọi $O$ là giao điểm của hai đường chéo $AC$ và $BD$.

a) Chứng minh rằng $OA.OD = OB.OC$. 

b) Đường thẳng qua $O$ vuông góc với $AB$ và $CD$ theo thứ tự tại $H$ và $K$.

Chứng minh rằng $\dfrac{OH}{OK} = \dfrac{AB}{CD}$

Lời giải chi tiết

a) Vì $AB // CD$ (giả thiết)

Áp dụng định lí:Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

$\Rightarrow ∆AOB ∽ ∆COD$ 

$\Rightarrow \dfrac{OA}{OC} = \dfrac{OB}{OD}$ (cặp cạnh tương ứng tỉ lệ)

$\Rightarrow  OA.OD = OC.OB$

b) Theo câu a) ta có $∆AOB ∽ ∆COD$ nên $\dfrac{OA}{OC} = \dfrac{AB}{CD}$  (1)

Xét $∆AOH$ và $∆COK$ có:

$\widehat{AHO} = \widehat{CKO} = {90^o}$

$\widehat {HOA} = \widehat {K{\rm{O}}C}$ (đối đỉnh)

$\Rightarrow ∆AOH ∽ ∆COK$ (g-g)

$\Rightarrow \dfrac{OH}{OK}= \dfrac{OA}{OC}$  (2) (cặp cạnh tương ứng tỉ lệ)

Từ (1) và (2) $\Rightarrow \dfrac{OH}{OK} = \dfrac{AB}{CD}$