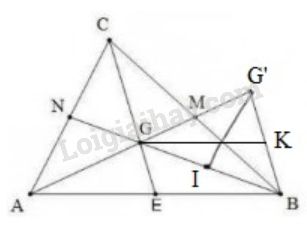
Bài 30 trang 67 SGK Toán 7 tập 2

Đề bài

Gọi $G$ là trọng tâm của tam giác $ABC$. Trên tia $AG$ lấy điểm $G’$ sao cho $G$ là trung điểm của $AG’$.

a) So sánh các cạnh của tam giác $BGG’$ với các đường trung tuyến của tam giác $ABC.$

b) So sánh các đường trung tuyến của tam giác $BGG’$ với các cạnh của tam giác $ABC.$

Lời giải chi tiết

a) So sánh các cạnh của $∆BGG’$ với các đường trung tuyến của $∆ABC.$

Gọi $M, N, E$ lần lượt là trung điểm của $BC, CA, AB.$

- Vì $G$ là trọng tâm của $∆ABC \Rightarrow GA =\dfrac{2}{3}AM$

Mà $GA = GG’$ ($G$ là trung điểm của $AG’$)

  $\Rightarrow GG' = \dfrac{2}{3} AM$

- Vì $G$ là trọng tâm của $∆ABC$ $\Rightarrow GB = \dfrac{2}{3} BN$

- Ta có:  

$GM =\dfrac{1}{2} AG$ (do $G$ là trọng tâm) và $AG = GG'$ (giả thiết)

$\Rightarrow GM = \dfrac{1}{2} GG'$, do đó $MG=MG'.$

Xét $∆GMC$ và $∆G’MB$ có: 

+) $GM = MG'$ (chứng minh trên)

+) $MB = MC$ ($M$ là trung điểm của $BC$)

+) ${\widehat {GMC} = \widehat {G'MB}}$ (hai góc đối đỉnh)

Vậy $∆GMC=∆G’MB$ (c.g.c)

 $\Rightarrow BG' = CG$ (Hai cạnh tương ứng)

Mà $CG = \dfrac{2}{3}  CE$ ($G$ là trọng tâm tam giác $ABC$) 

 $\Rightarrow BG' = \dfrac{2}{3} CE$

Vậy $GG' = \dfrac{2}{3}AM,GB = \dfrac{2}{3}BN,G'B = \dfrac{2}{3}CE$

Hay mỗi cạnh của $∆BGG’$ bằng  $\dfrac{2}{3}$ đường trung tuyến của $∆ABC.$

b) So sánh các đường trung tuyến của $∆BGG’$ với các cạnh của $∆ABC.$

- Ta có: $BM$ là đường trung tuyến $∆BGG’$

Mà $M$ là trung điểm của $BC$ nên $BM = \dfrac{1}{2} BC$.

Gọi $I$ là trung điểm $BG$ 

Vì $IG = \dfrac{1}{2} BG$ (do $I$ là trung điểm $BG$)

$GN = \dfrac{1}{2}BG$ ($G$ là trọng tâm)

$\Rightarrow  IG = GN$

Xét  $∆IGG’$ và $∆NGA$ có:

+) $IG = GN$ (chứng minh trên)

+) $GG' = GA$ (giả thiết)

+) $\widehat {IGG'} = \widehat {NGA}$ (hai góc đối đỉnh)

Vậy $∆IGG’ = ∆NGA$ (c.g.c) 

$\Rightarrow  IG' = AN$ (hai cạnh tương ứng)

$\Rightarrow  IG' = \dfrac{{AC}}{2}$

- Gọi $K$ là trung điểm $BG'$ $\Rightarrow  GK$ là trung tuyến của $∆BGG’$

Vì $GE = \dfrac{1}{2} GC$ ($G$ là trọng tâm tam giác $ABC$)

$BG' = GC$ (chứng minh trên)

$\Rightarrow  GE =\dfrac{1}{2} BG'$

Mà $K$ là trung điểm $BG’$ $\Rightarrow KG’ = EG$

Vì $∆GMC = ∆G’MB$ (chứng minh trên)

$\Rightarrow$   $\widehat {GCM} = \widehat {G'BM}$ (hai góc tương ứng)

Mà 2 góc này ở vị trí so le trong

$\Rightarrow  CE // BG’$ $\Rightarrow$   $\widehat {AGE} = \widehat {AG'B}$ (2 góc đồng vị)

Xét $∆AGE$ và $∆GG’K$ có:

+) $EG = KG’$ (chứng minh trên)

+) $AG = GG'$ (giả thiết)

+) $\widehat {AGE} = \widehat {AG'B}$ (chứng minh trên)

Vậy $∆AGE = ∆GG’K$ (c.g.c)

$\Rightarrow AE = GK$ ( 2 cạnh tương ứng)

Mà $AE = \dfrac{1}{2}AB$

$\Rightarrow  GK =  \dfrac{1}{2} AB$

Vậy $BM = \dfrac{1}{2}BC,G'I = \dfrac{1}{2}AC,GK = \dfrac{1}{2}AB$ 

Hay mỗi đường trung tuyến của $∆BGG’$ bằng một nửa cạnh của tam giác $ABC$